インテジャーズ

INTEGERS

数、特に整数に関する記事。

わにたろうとわに子のぼうけん

その他

これは私が1997年12月18日に執筆した物語を記録するものである。

登場人物

わにたろう
わに子
わにみ（おかあさん）
わにさぶろう（おとうさん）
ちゅん（すずめ）
スーパーきょうわくわるわるくじら王

f:id:integers:20190814202953p:plain

わにたろうとわに子のぼうけん


「わにたろうくんおきて」


わに子はぼうけんのすきな女のわにです。


「またぼうけんか。」


わにたろうはねむそうに言いました。


「わるい。」


わに子がおこって言いました。


「そうだ海できょうそうしない。」


わに子がたずねました。


「うん。いくよ。」


わにたろうが答えました。


「じゃあ行こう。」


わに子がうれしそうに言いました。


二人は北のしままできょうそうしましたが、わにたろうがとちゅうで、


「もうおよげないよう。」


となきました。


わに子は


「もう、しょうがないな。」


といってせなかにのせました。


なんとかしままでつきました。


二人はつかれたのでねむってしまいました。


「わに子なんか音しない。」


わにたろうが言いました。


「え、あ火山だよ。」


f:id:integers:20190814203123p:plain


二人はおきました。


二人はいそいで南のしまにいこうとしました。


二人は海に入っておよぎました。


南のしまにつきました。


「あれ、火山は、ゆめだったの。」


二人はいっしょに言いました。


「でもおよげたじゃん。」


わに子が言いました。


「まあね。」


わにたろうがじまんそうに言いました。


「あ、はちのすふんじゃった。」


とわにたろうが言いました。


f:id:integers:20190814203238p:plain


二人はおおいそぎでにげ回りました。


はちはにげました。でも、


「いたいよー。」


わにたろうがさされてしまいました。


がすぐなおりました。


そこへすずめのちゅんがきました。


「いっしょにあそばない。」


わに子が言いました。


「いいよ。」


ちゅんが言いました。


「遠足にいくんじゃなかったの。」


「ちゅうしになったの。」


「じゃんけんしない。」


「でももうおそいから帰るよ。」


ちゅんが言いました。


「バイバイ。」


わに子とわにたろうが言いました。


二人はふねにのって家に帰りました。


f:id:integers:20190814203403p:plain


f:id:integers:20190814203622p:plain


「今日はすごいぼうけんだったね。」


わに子が言いました。


「ねえ、おかあさん。」


わに子が言いました。


「なんだい。」


おかあさんのわにみが言いました。


「あのね 今日、すごいぼうけんしたんだよ。」


わにたろうが言いました。


f:id:integers:20190814203453p:plain


「もう わたしがいおうとしたのに。」


わに子がおこりました。


「けんかしちゃだめよ。」


とおかあさんにいわれ


「はい。」


と二人はちいさいこえで言いました。


二人は家ではなく外でまたねてしまいました。


f:id:integers:20190814203424p:plain


「ねえ、海にもぐらない。」


わにたろうは言いました。


「うん、いいよ。」


わに子が言いました。


二人はゆめのなかで海にもぐりました。


「ねえねえなにか光ってるよ、いってみない。」


「うんそうだね」


「あっおかねだ。」


f:id:integers:20190814203524p:plain


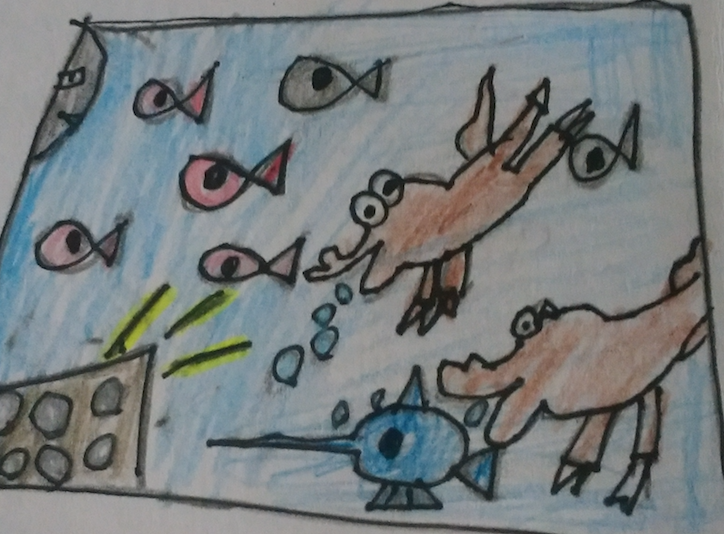
二人はよろこんだけどそのとき


「うわー。」


f:id:integers:20190814203824p:plain


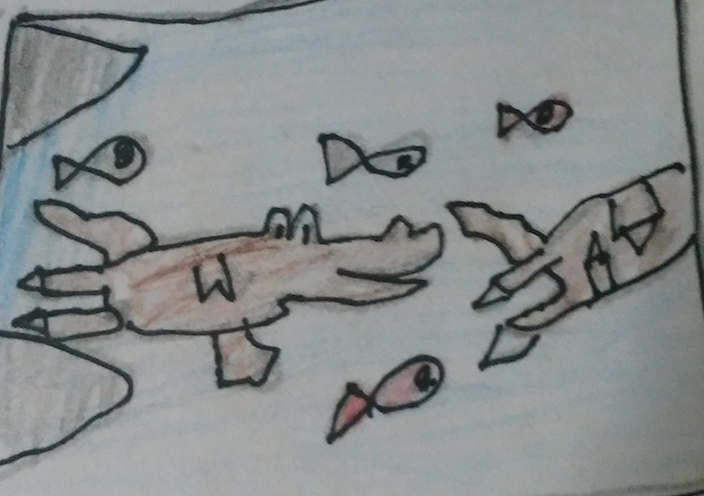
二人はスーパーきょうわくわるわるくじら王にくわれてしまいました。


二人はおなかのなかでないているとさかなたちがきました。


f:id:integers:20190814203845p:plain


「どうしたんだい、スーパーきょうわくわるわるくじら王にたべられたのかい。」


わにたろうが言いました。


「うんそうなんだよ。」


さかなたちもないてしまいました。


「そうだ、計画をた(て)るんだ。」


さかなたちとわに子とわにたろうは計画をたてています。


f:id:integers:20190814203701p:plain


「まずしんでいるさかなをつなげてくじらのおなかをたたけばいいと思うけど。」


わにたろうがしんけんになって言いました。


「どうやってつなげるの。」


わに子が言いました。


みんな考えていると


「そうだ、くじらのよだれでひっつけたらいいんだよ。」


さかなたちが言いました。


みんな一づつつくりました。


たたいてみるとまるいあながあいてみんなあなからでると


「やったー。」


とみんな言いましたが、そこはまだくじらのはのところでした。


みんながっかりしたけどつぎのさくせんをきめました。


「わにたろうくんがくじらのはをかんではをおったらいいと思うけど。」


とさかなたちが言いました。


みんなでれました。その時二人はゆめからおきました。


「またゆめだったのか」


二人はいっしょに言いました。


そのときおとうさんのわにさぶろうがしごとから帰ってきて


「こらなにしてんの。」


とおこられました。


「ごめんなさい。」


二人はおとうさんにいってわらいながら帰りました。


f:id:integers:20190814203917p:plain

Chebyshevによる(素数計数関数についての)Legendre予想の否定的解決について

定理解説

Chebyshevは素数定理の弱い版である

\displaystyle c_1\frac{x}{\log x} \leq \pi(x) \leq c_2\frac{x}{\log x}

を示しており(c_1, c_2は正の定数), 極限\displaystyle \lim_{x\to \infty}\frac{\pi(x)\log x}{x}が存在するならば1でなければならないということを示していました.

実は彼はLegendre予想の否定という仕事もやっています(xに関する漸近挙動はx\to \inftyを考える).

Legendre予想 (1798/1808) \pi(x)は
\displaystyle \pi(x)=\frac{Bx}{\log x-A+o(1)}\tag{1}
を満たし, 更にA=1.08366..., B=1が成り立つであろう.

とりあえず, これは素数定理より強い予想ですが, Aの値は間違えており, Chebyshevが次を示しました.

定理 (Chebyshev, 1848) (1)が成り立つのであれば, A=B=1でなければならない.

実はGaussは正しく予想していたようです. Chebyshevは\zeta^{(m)}(s)のs\to 1+0の挙動を使って少し強い形で定理を証明し, 実際に極限が存在するという難しい部分はde la Valée Poussinが1899年に証明しています(素数定理の証明は1896年).

さて, 実は上記Chebyshevの定理は非常に簡単に証明できることがPintzによって指摘されています.

J. Pintz, On Legendre's prime number formula, Amer. Math. Monthly 87 (1980), 733-735.

その証明を紹介したいのですが, ちょうど私が執筆した素数定理の証明の本

note.mu

の中で示されている公式達を使わせていただくと簡単に紹介できるのでそうさせていただきます. この本では第一世代・第二世代・第三世代のビッグ・オー不等式があって, 第三世代まで行くと素数定理の証明が可能となったということが書かれています(なお, この記事ではビッグ・オー不等式としてではなく漸近公式のみを考えれば十分です).

一言で述べると, 上記Chebyshevの定理は第二世代の(von-Mangoldt関数版の)Mertensの第一定理から瞬殺されます. Pintzが

So it is curious that Legendre's conjecture (1.2) had remained open for 40 years.

とコメントしているのは納得です.

PintzによるChebyshevの定理の証明

\Lambda(n)はvon-Mangoldt関数(素数定理本 定義6.9). \psi(x)は第二Chebyshev関数(素数定理本 定義6.13). 実際には次を示す.

定理 (Pintz) \psi(x)が
\displaystyle \psi(x)=Cx+\frac{(D+o(1) )x}{\log x}\tag{2}
を満たすのであれば, C=1かつD=0でなければならない.

補題 f(x)=o(g(x))であり, f(x), g(x)は任意のx\geq aに対して[a,x]でリーマン積分可能であるとする(a \in \mathbb{R}). \int_a^xg(t)\mathrm{d}t\to\infty \ (x \to \infty)であれば,
\displaystyle \int_a^xf(t)\mathrm{d}t=o\left(\int_a^xg(t)\mathrm{d}t\right)
が成り立つ.

証明. 任意に\varepsilon > 0をとり, t\geq cであれば \left|f(t)\right|\leq \varepsilon g(t)が成り立つとする. このとき,

\displaystyle \left|\int_a^xf(t)\mathrm{d}t\right| \leq \int_a^c\left|f(t)\right|\mathrm{d}t+\int_c^x\left|f(t)\right|\mathrm{d}t\leq A+\varepsilon\int_c^x\left|g(t)\right|\mathrm{d}t

と評価できる. ここで, A:=\int_a^c\left|f(t)\right|\mathrm{d}t. 仮定よりxが十分大きければ

\displaystyle \left.\left|\int_a^xf(t)\mathrm{d}t\right|\right/\int_a^xg(t)\mathrm{d}t \leq 2\varepsilon

とできる. Q.E.D.

Pintzの定理からChebyshevの定理が出ること(この部分は基本的ということでPintzの論文には書かれていない): Abelの総和公式(素数定理本 命題5.1)においてa_n=\frac{\Lambda(n)}{\log n}, \varphi(x)=\log xとすると, \displaystyle \sum_{2\leq n\leq x}a_n\varphi(n)=\psi(x)であり,

\displaystyle \sum_{2\leq n \leq x}a_n=\sum_{p^k\leq x}\frac{\log p}{k\log p}=\sum_{k=1}^{\infty}\frac{1}{k}\pi(x^{\frac{1}{k}}),

\displaystyle \sum_{k=2}^{\infty}\frac{1}{k}\pi(x^{\frac{1}{k}}) \leq\sum_{k=2}^{[\log_2x]}\sqrt{x}=O(\sqrt{x}\log x)=o\left(\frac{x}{\log^2x}\right)

なので, 補題より

\displaystyle \psi(x)=\pi(x)\log x+o\left(\frac{x}{\log x}\right)-\int_2^x\frac{\pi(t)}{t}\mathrm{d}t+o\left(\int_2^x\frac{\mathrm{d}t}{\log^2t}\right)

を得る. Chebyshevの定理を証明するために(1)が成立すると仮定する. \frac{1}{1-X}=1+X+o(X), (X\to 0)に注意すれば,

\displaystyle \pi(x)\log x=\frac{Bx}{1-\frac{A+o(1)}{\log x}}=Bx+\frac{B(A+o(1) )x}{\log x}+o\left(\frac{x}{\log x}\right).

\pi(t)=\frac{Bt}{\log t}+O\left(\frac{t}{\log^2t}\right)より, 素数定理本 補題4.4によって

\displaystyle \int_2^x\frac{\pi(t)}{t}\mathrm{d}t=B\int_2^x\frac{\mathrm{d}t}{\log t}+O\left(\int_2^x\frac{\mathrm{d}t}{\log ^2t}\right).

素数定理本 補題4.5(4), (6)より

\displaystyle O\left(\int_2^x\frac{\mathrm{d}t}{\log^2t}\right)=o\left(\frac{x}{\log x}\right), \quad \int_2^x\frac{\pi(t)}{t}\mathrm{d}t=\frac{Bx}{\log x}+o\left(\frac{x}{\log x}\right).

である. 以上をまとめると,

\displaystyle \psi(x)=Bx+\frac{(B(A-1)+o(1) )x}{\log x}

の成立がわかった. よって, Pintzの定理が正しければ, B=1およびB(A-1)=0が従い, A=B=1となる. Q.E.D.

Pintzの定理の証明. (2)の成立を仮定する. 素数定理本 命題6.18(17)より

\displaystyle \sum_{n\leq x}\frac{\Lambda(n)}{n}=\log x+O(1)\tag{3}

が成り立つ(今は(2)の成立を仮定しているため \psi(x)=O(x)が使用可能であり, 従って命題6.18(17)の証明(=シャピロのタウバー型定理の証明)で比較的難しかった部分の議論は全て不要であることに注意). また, Abelの総和公式をa_n=\Lambda(n) \ (n\geq 2), \varphi(x)=\frac{1}{x}として適用すれば

\displaystyle \sum_{n\leq x}\frac{\Lambda(n)}{n}=\frac{\psi(x)}{x}+\int_2^x\frac{\psi(t)}{t^2}\mathrm{d}t

が得られる. 仮定より右辺は

\displaystyle O(1)+\int_2^x\frac{C+\frac{D+o(1)}{\log t}}{t}\mathrm{d}t=C\log x+(D+o(1) )\log \log x\tag{4}

が成り立つ. ここで,

\displaystyle \int_2^x\frac{\mathrm{d}t}{t\log t}=\log \log x-\log \log 2

と補題を使った. (3), (4)が両立するためには, C=1, D=0でなければならない. Q.E.D.

PID

整数 整数-19 整数-43 整数-67 整数-163

twitterでブログ記事のお題を募集したところ、みぽさんから次のようなお題をいただきました。

PIDについて何を書こうかなあと思案したところ、むしろユークリッド整域との関係性について書きたくなってきました。なので、タイトル詐欺ではありますがユークリッド整域が主役のお話を書かせていただこうと思います。

この記事の執筆に先立ってツイキャス放送を行っています(動画は五つ)。
PID講義 - 二本松せきゅーん (@integers_blog) - TwitCasting

そこでの内容に沿って執筆致します(一部カット)。メインは定理2.7です。

本文

1 ユークリッド整域と単項イデアル整域

1.1 可換環
Rは基本的に1をもつ可換環(1\neq 0)とする.

1.2 整域
Rにおいてa,b\in R, ab=0 \Longrightarrow a=0 or b=0が成り立つとき, Rは整域であるという.

1.3 ユークリッド整域
整域Rがユークリッド整域であるとは写像\varphi\colon R\setminus\{0\} \to \mathbb{N}_0であって以下の二条件を満たすものをいう*1. 条件1. 任意のa,b\in R, b\neq 0に対して或るq,r\in Rが存在してa=bq+rなる関係があり, r=0または\varphi(r) < \varphi(b)が成り立つ. 条件2. 任意のa,b \in R\setminus\{0\}に対して\varphi(a)\leq \varphi(ab)が成り立つ.

1.4 ユークリッド整域の例
体K; \varphi(a):=1 \ (a\in K^{\times}).
有理整数環\mathbb{Z}; \varphiは通常の絶対値.
体Kに対する一変数多項式環K[x]; \varphi(f):=\deg(f) \ (f\neq 0).

1.5 単項イデアル整域(PID)
整域RがPIDであるとは, 任意のRのイデアルが単項イデアルであるときにいう.

命題1.6 ユークリッド整域はPIDである.
証明: Rが\varphiでユークリッド整域であるとする. Rの0でないイデアルIを任意にとる. 集合\{b\in I\setminus\{0\} \mid \varphi(b)=\min_{a\in I\setminus\{0\}}\varphi(a)\}から元bを一つとる. bR \subset I. 任意にa \in Iをとる. a=bq+rが成り立つような或るq,r\in Rが存在して, r=0または\varphi(r) < \varphi(b)が成り立つ(1.3条件1). Iはイデアルなのでr=a-bq \in I. よって, r\neq 0とすると\varphi(b)の最小性に矛盾する. 従って, r=0であり, a=bq \in bR, すなわちI \subset bR. Q.E.D.

事実1.7 逆は一般に成り立たない.

2 二次体の整数環

2.1 二次体
m \neq 0,1を無平方数とする. \mathbb{Q}(\sqrt{m}) := \{a+b\sqrt{m} \mid a,b \in \mathbb{Q}\}. m > 0のとき実二次体, m < 0のとき虚二次体という.

2.2 二次体の整数環
二次体\mathbb{Q}(\sqrt{m})の整数環\mathcal{O}_{\mathbb{Q}(\sqrt{m})}はm \equiv 2,3\pmod{4}のとき \mathcal{O}_{\mathbb{Q}(\sqrt{m})}=\mathbb{Z}+\mathbb{Z}\sqrt{m}, m\equiv 1 \pmod{4}のとき \mathcal{O}_{\mathbb{Q}(\sqrt{m})}=\mathbb{Z}+\mathbb{Z}\frac{1+\sqrt{m}}{2}である.

2.3 ノルム写像
\alpha=a+b\sqrt{m} \in \mathbb{Q}(\sqrt{m}), N_{\mathbb{Q}(\sqrt{m})}(\alpha):=a^2-mb^2. N_{\mathbb{Q}(\sqrt{m})}(\alpha\beta)=N_{\mathbb{Q}(\sqrt{m})}(\alpha)N_{\mathbb{Q}(\sqrt{m})}(\beta). \alpha \in \mathcal{O}_{\mathbb{Q}(\sqrt{m})} \Longrightarrow N_{\mathbb{Q}(\sqrt{m})}(\alpha) \in \mathbb{Z}.

2.4 虚二次体の単数群
\mathcal{O}_{\mathbb{Q}(\sqrt{-d})}^{\times}=\{\pm1, \pm i\}, i=\sqrt{-1}.
\mathcal{O}_{\mathbb{Q}(\sqrt{-d})}^{\times}=\{\pm1, \pm \omega, \pm \omega^2\}, \omega=\frac{-1+\sqrt{-3}}{2}.
\mathcal{O}_{\mathbb{Q}(\sqrt{-d})}^{\times}=\{\pm1\}, d\neq 1,3, d > 0.

定理2.5 (Baker-Stark-Heegner)
虚二次体\mathbb{Q}(\sqrt{-d})がPIDとなるのはd=1,2,3,7,11,19,43,67,163の九つである.

証明は例えば参考文献[H]を参照のこと.

定理2.6 d=1,2,3,7,11に対する\mathcal{O}_{\mathbb{Q}(\sqrt{-d})}はノルム写像によってユークリッド整域となる.

定理2.7 d=19,43,67,163に対する\mathcal{O}_{\mathbb{Q}(\sqrt{-d})}はPIDではあるが, ユークリッド整域ではない.

これは事実1.7の裏付けになっている. 動画では§2は後少し続く.

3 定理2.6の証明

3.1 d=1,2の場合.
1.3の条件1のみが非自明である. \alpha, \beta \in \mathcal{O}_{\mathbb{Q}(\sqrt{-d})}, \beta \neq 0をとり, \alpha/\beta=x+y\sqrt{-d}とおく. \left|x-u\right|\leq 1/2, \left|y-v\right|\leq 1/2なるu,v \in \mathbb{Z}をとる. q:=u+v\sqrt{-d} \in \mathcal{O}_{\mathbb{Q}(\sqrt{-d})}. r:=\alpha-\beta q\in \mathcal{O}_{\mathbb{Q}(\sqrt{-d})}. N_{\mathbb{Q}(\sqrt{-d})}(r)=N_{\mathbb{Q}(\sqrt{-d})}( (x-u)+(y-v)\sqrt{-d})N_{\mathbb{Q}(\sqrt{-d})}(\beta)なので, N_{\mathbb{Q}(\sqrt{-d})}( (x-u)+(y-v)\sqrt{-d})=(x-u)^2+d(y-v)^2 < 1であればよいが, 今はd=1, 2なので成立する.

3.2 d=3,7,11の場合(-d \equiv 1 \pmod{4}に注意).
\alpha/\beta=x+y\sqrt{-d}とおく. \left|x-u\right|\leq 1/2, \left|y-v\right|\leq 1/4なるu,v \in \frac{1}{2}\mathbb{Z}, 2u\equiv 2v \pmod{2}をとる(x \in [m, m+1], y\in [n, n+1]のとき(m,n \in \mathbb{Z}), u=m+1/2, v=n+1/2としてもq \in \mathcal{O}_{\mathbb{Q}(\sqrt{-d})}が成り立つことに注意). 3.1と同様に考えて(x-u)^2+d(y-v)^2 \leq \frac{1}{4}+\frac{d}{16}. \frac{1}{4}+\frac{d}{16} < 1 \Longleftrightarrow d < 12である. Q.E.D.

4 定理2.7の証明. R: 整域. R\setminus \{0\}は積閉集合となっている.

4.1 A \subset R\setminus \{0\}が積イデアルであるとは, A\cdot (R\setminus \{0\}) \subset Aが成り立つことである. すなわち, 任意のa \in A, r \in R\setminus \{0\}に対してar \in Aが成立すること.

4.2 A \subset Rに対してA^d \subset AをA^d:=\{b \in A \mid {}^{\exists} a \in R \ \text{s.t.} \ a+bR \subset A\}と定義する.

4.3 Aが積イデアルであればA^dも積イデアルである.

証明: b \in A^d, q \in R\setminus \{0\}に対してbq \in A^dを示せばよい. Aが積イデアルなのでbq \in Aである. また, b \in A^dであることからa+bR \subset Aなるa \in Rが存在する. このとき, a+bqR \subset a+bR \subset A. よって, bq \in A^d. Q.E.D.

4.4 A_1 \subset A_2であればA_1^d \subset A_2^d.

証明: b \in A_1^dをとると, a+bR \subset A_1 \subset A_2なるa \in Rが存在する. これとb \in A_1 \subset A_2からb \in A_2^d. Q.E.D.

定理4.5 (Motzkin [M])
整域Rがユークリッド整域であるための必要十分条件は積イデアルの減少列R \setminus \{0\} = A_0 \supset A_1 \supset A_2 \supset \cdotsであって, 任意のi \geq 0に対してA_i^d \subset A_{i+1}が成り立ち, \bigcap_{i=0}^{\infty}A_i=\varnothingであるようなものが存在することである.

4.6 \Longrightarrowの証明. Rは\varphi\colon R\setminus \{0\} \to \mathbb{N}_0によりユークリッド整域であるとする. i \geq 0に対して, A_i:=\{a \in R\setminus\{0\} \mid \varphi(a) \geq i\}とする. R\setminus \{0\}=A_0およびA_i \supset A_{i+1} \ ({}^{\forall}i \geq 0)は定義から自明. 1.3条件2よりA_iは積イデアル. 任意にb \in A_i^dをとってb \in A_{i+1}を示す. a+bR \subset A_iなるa \in Rが存在する. また, 1.3条件1よりa=bq+rなるq,r \in Rが存在してr=0または\varphi(r) < \varphi(b)が成り立つ. r=a-bq \in A_i \subset R\setminus \{0\}よりr \neq 0. よって, \varphi(b) > \varphi(r) \geq i. すなわち, \varphi(b) \geq i+1でこれはb \in A_{i+1}を示している. 従ってA_i^d \subset A_{i+1} \ ({}^{\forall}i \geq 0). \bigcap_{i=0}^{\infty}A_i\neq \varnothingと仮定し, そこから元aを取る. \varphi(a)=jとするとa \not\in A_{j+1}となってaの取り方に矛盾. よって\bigcap_{i=0}^{\infty}A_i=\varnothingである.

4.7 \Longleftarrowの証明. 写像R\setminus\{0\}\to \mathbb{N}_0をa \in A_i\setminus A_{i+1}に対して\varphi(a):=iと定義する(\bigcap_{i=0}^{\infty}A_i=\varnothingよりwell-defined). a, b\in R\setminus\{0\}を任意にとって\varphi(a)=iとすると, a \in A_iおよびA_iが積イデアルであることからab \in A_iである. よって, \varphi(ab) \geq i = \varphi(a)となって1.3条件2が確認された. 条件1を確認するためにa, b \in R, b\neq 0を任意にとる. 0 \in a+bRであれば, 或るq \in Rが存在してa=bqが成り立ちr=0のケースとして条件1が成立している. そこで, a+bR \subset R\setminus \{0\}とする. \bigcap_{i=0}^{\infty}A_i=\varnothingなので, a+bR\subset A_iおよびa+bR \not\subset A_{i+1}なるi \geq 0が存在する. また, b \in A_j\setminus A_{j+1}なるj \geq 0も存在する. j \leq iと仮定するとa+bR \subset A_i \subset A_jであり, これはb \in A_j^d \subset A_{j+1}を意味するからjの取り方に矛盾する. 従って, j > iである. 今, r:=a-bq \in A_i\setminus A_{i+1}なるq \in Rをとることができるが, \varphi(r)=i < j=\varphi(b)を得る. Q.E.D.

4.8 R: 整域. A \subset Rに対してA\setminus A^d=\{b \in A \mid {}^{\forall}a \in R, {}^{\exists}c \in R\setminus A \ \text{s.t.} \ b \mid a-c\}.

証明: b \in A\setminus A^d \Longleftrightarrow 「{}^{\exists}a \in R, a+bR\subset A」でない \Longleftrightarrow {}^{\forall}a \in R, a+bR \not\subset A. a+bR\not\subset A \Longleftrightarrow {}^{\exists}q \in R \ \text{s.t.} \ a+bq \not\in A \Longleftrightarrow {}^{\exists}q \in R, {}^{\exists}c \in R\setminus A \ \text{s.t.} \ a+bq=c \Longleftrightarrow {}^{\exists}c \in R\setminus A \ \text{s.t.} \ b \mid a-c. Q.E.D.

4.9 A_0:=R\setminus \{0\}とする. このとき, A_0^d=R\setminus(R^{\times} \cup \{0\}).

証明: R\setminus A_0=\{0\}であるので, 4.8によりb \in A_0\setminus A_0^d \Longleftrightarrow {}^{\forall}a \in Rに対してb \mid a \Longleftrightarrow b \in R^{\times}. Q.E.D.

4.10 a\in R. b\in A_0^dがaのサイド因子であるとは, 或るe \in R^{\times} \cup \{0\}が存在してb \mid a-eが成り立つことである.

4.11 b \in A_0^dが普遍サイド因子であるとは, 任意のa \in Rに対してbがaのサイド因子であることとする.

4.12 bが普遍サイド因子であればbRは極大イデアルである.

証明: 定義よりb \in A_0^dが普遍サイド因子であるための必要十分条件は任意のa \in Rに対してe \in R^{\times} \cup \{0\}が存在してa\bmod{b}=e\bmod{b}が成り立つことである. つまり, R/bRの各元はR^{\times}\cup\{0\}に代表元をとることができ, R/bRは体である. Q.E.D.

4.13 A_0^{dd}=A_0^d \setminus \{\text{普遍サイド因子全体}\}.

証明: 4.8, 4.9よりA_0^{d}\setminus A_0^{dd}=\{b \in A_0^d \mid {}^{\forall}a \in R, {}^{\exists}e \in R^{\times}\cup\{0\} \ \text{s.t.} \ b\mid a-e\}=\{\text{普遍サイド因子全体}\}. Q.E.D.

系4.14 普遍サイド因子を有しない整域は体を除いてユークリッド整域ではない.

証明: 4.13より普遍サイド因子を有しない整域RはR\setminus\{0\}=A_0とするとA_0^{dd}=A_0^dを満たす. もしRがユークリッド整域であれば定理4.5の積イデアル減少列R \setminus \{0\} = A_0 \supset A_1 \supset A_2 \supset \cdotsが存在する. A_0^d \subset A_1と4.4よりA_0^{dd}\subset A_1^dであるが, A_0^{dd}=A_0^dとA_1^d\subset A_2よりA_0^d\subset A_2が得られる. これを繰り返せばA_0^d \subset \bigcap_{i=0}^{\infty}A_i=\varnothingとなるため, A_0^d=\varnothing. 4.9よりこれはR=R^{\times}\cup\{0\}を意味し, Rはすなわち体である. Q.E.D.

4.15 K=\mathbb{Q}(\sqrt{-d}), \ d=19, 43, 67, 163とする. -d \equiv 1 \pmod{4}に注意. \mathcal{O}_{K}=\mathbb{Z}+\mathbb{Z}\frac{1+\sqrt{-d}}{2}が普遍サイド因子を有しないことを示せばよい.

4.16 2.4より\mathcal{O}_K=\{\pm1\}.

4.17 2,3は\mathcal{O}_Kの既約元である.

証明: N_K(2)=4, N_K(3)=9. \alpha \mid 2 (resp. 3)であればN_K(\alpha) \mid 4 (resp. 9)でなければならない. \alpha=a+b\sqrt{-d} (a, b \in \mathbb{Z})と書ける場合を先に考える. N_K(\alpha)=a^2+db^2が4 (resp. 9)を割り切ればb=0であり, a^2=1 or 4 (resp. 1 or 9). すなわち, \alpha = \pm 1 or \pm 2 (resp. \pm 1 or \pm 3)がわかる. \alpha=a+\frac{1}{2}+(b+\frac{1}{2})\sqrt{-d} (a, b \in \mathbb{Z})と書ける場合はこのような整除は起き得ないことを示す. N_K(\alpha)=a^2+a+d(b^2+b)+\frac{1+d}{4}である. a^2+a, b^2+b \geq 0なので, d\geq 43のときは\frac{1+d}{4}\geq 11なので4, 9を割ることはできない. d=19の場合も\frac{1+d}{4}=5であり, この時点で4は割り切れない. 9を割るとしたらb=0でなければならず結局a^2+a+5=9とならなければならないが, そのようなaは存在しない. Q.E.D.

4.18 2のサイド因子は\pm 2, \pm 3のみである.

証明: b \in A_0^d, すなわち, b \not\in \mathcal{O}_K^{\times}\cup\{0\}=\{0, \pm 1\}が2のサイド因子であれば, 或るe \in \{0, \pm 1\}が存在して, b \mid 2-eが成り立つ. すなわち, b \mid 1 or 2 or 3である. 今, b \mid 1は不可能. 従って, b \mid 2 or 3であり, 4.17からb=\pm 2 or \pm 3がわかった. Q.E.D.

4.19 \pm 2, \pm 3は\frac{1+\sqrt{-d}}{2}のサイド因子ではない.

証明: b=\pm 2, \pm 3が\frac{1+\sqrt{-d}}{2}のサイド因子になったと仮定すると, b \mid \frac{1+\sqrt{-d}}{2}-eが或るe \in \{0, \pm 1\}に対して成立する. すなわち, 有理整数a, cが存在して, b(a+c\frac{1+\sqrt{-d}}{2})=\frac{\pm 1+\sqrt{-d}}{2} or \frac{3+\sqrt{-d}}{2}が成り立つ. 両辺二倍すると, 左辺はb(2a+c+c\sqrt{-d})で右辺の\sqrt{-d}の係数は1. つまり, bc=1が成り立つ. それは不可能な言明である.

4.20 4.18+4.19より\mathcal{O}_Kは普遍サイド因子を持たない. よって, 系4.14より\mathcal{O}_Kはユークリッド整域ではないことが示された. Q.E.D.

参考文献

[H] 平山 楓馬, 類数1の虚二次体, 第72回灘校文化祭.
[I] icqk3氏による補足, http://searial.web.fc2.com/aerile_re/eucliddomain.html
[M] T. Motzkin, The Euclidean Algorithm, Bull. Amer. Math. Soc. 55 (1949), 1142-1146.

*1:本稿ではこの定義を採用する.