butchi氏が卒業論文で研究したという平面2進数(=物智(butchi)数)というものを何度かbutchi氏から聞いたことがありました。
butchi氏自身による解説等がHPにあります:平面的2進数(Butchi数)
だふやふさんという方がこのbuichi数に関する記事*1を書いているのを読んで、自分でも一度考えておこうと思いました。
butchi数とは何かというと、基本的には、数というよりは進法や
進法、
進法などと同じく、整数の一つの表示法のことを言います(butchi数表示)。それは名前の通り平面的に広がる2進表記(
,
が平面的に広がる)であり、
は白、
は黒と思うことによって整数を可視化することができます。butchi数表示で得られるドット絵は最初のリンクにある物智数ビューワーで簡単に見ることができます。また、卒論に掲載されている
のbutchi数表示のドット絵は中々イカします(butchi氏に許可を頂いたので掲載します。butchi氏に感謝致します)。
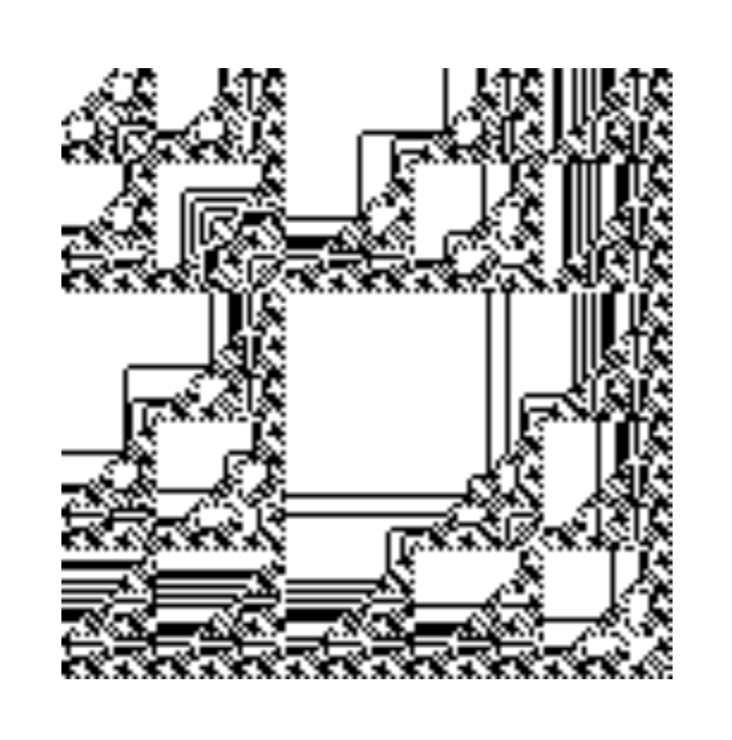
butchi数表示はの元だけではなく、
進整数環
の元に対しても適用できます(上記
は
の元です)。一方、
のbutchi数表示は全てのドット絵を実現するわけではありません。だふやふ氏の記事では必ずしも
の元のbutchi数表示ではないようなドット絵(ただし左方向と上方向に伸びるもの*2 )のこともbutchi数と呼んでいます(最初のリンクの概要の最後の行にも書いてあります)。
つまり、butchi数表示(butchi数-表示ではなくbutchi-数表示)によって数をドット絵として表現することができたので、逆にドット絵は数とみなそうということです。これによって新しい数体系ができそうな期待が生じます。この必ずしも進整数とは限らないドット絵に対応する元(定義はこの記事で行います)のことをbutchi数と呼ぶことにしましょう。
この記事ではbutchi数を構成して、butchi数の基本性質やbutchi数全体のなす集合の代数構造について記述します。
butchi数及びbutchi数表示の定義と基本性質
butchi氏に倣って
を
と表示します。
イデアルでの合同を記号
で表すことにすると、上記表示においては
なる形の合同で変形を行っていくことができます(基本変形)。
例えば、
は
と表示できます。
実は、最後の「のみを用いた表示」がbutchi数表示なのです。
から
までのbutchi数表示を書いておきますので、上の
の場合を真似てそれぞれ変形できることを確認してみてください(butchi数表示の厳密な定義は少し後に出てきます):
butchi数全体のなす集合には定義より可換環の構造が入りますが、butchi数表示の和については成分同士を足した後に基本変形を行うのが良いでしょう(筆算、繰り上がり):
積については多項式(冪級数)の積を用いて定義されますが、その定義から例えば次のようにbutchi数表示同士の積を計算できます:
証明. 帰納法で示す。のときは容易に確かめられる。
で正しいと仮定して
のときに証明する。
とのときも成立することが示された。 Q.E.D.
証明. 任意の自然数に対して
が成り立つことが帰納的に確かめられる:
よって、補題1の式の右辺をとおけば
が任意の自然数
に対して成り立つことがわかる。
であるから、
が成り立つ。従って、題意は示された。 Q.E.D.
補題2はのbutchi数表示が
となることを意味します。 以外の部分は全て
です。
このように、butchi整数のbutchi数表示はの個数が有限個とは限りません。
証明. まず、一意性を証明する。そのためには、を除いて
となり得ないことを示せばよい。そこで、上式が成立したと仮定して背理法で示す。すなわち、が存在して
が成り立つとする。このとき、両辺の係数がでない最低次数の項のうちの一つを比較すると、係数が左辺は
、右辺は偶数となって矛盾する。
次に存在性を証明しよう。を任意にとる。全ての係数が非負整数であるような形式的冪級数であって、
と合同であるようなものが存在することに注意する。実際、補題2の右辺を
とし、
とすると
は所望の冪級数となっている。従って、存在性の証明においてであると仮定してよい。
とする。各非負整数に対して、
に有限回基本変形を行うことによって、
と合同となるような
係数の多項式
が得られる(これは証明の前半部より一意的に存在する)。
より
なので(これは一意性からわかる)、
が存在する。すると、構成の仕方から
かつ、右辺の極限は係数の冪級数である。 Q.E.D.
例えば、
はのbutchi数表示ですが、
の個数を数えると確かに
個あり、一番下の行を見ると
の
進表示
になっています。また、補題2の直後に書いたのbutchi数表示の一番下の行は
の
における
進表示
になっています。
証明. 前半は基本変形において係数の総和が不変であることから従う。自然な埋め込み
を進整数の
進展開が
であるとき(
)、
で定める。このとき、のbutchi数表示の一番下の行は
の係数(すなわち、の
進展開係数
)が並んでいる。 Q.E.D.
証明. 代入写像
が準同型であることからわかる(butchi自然数はbutchi整数であることに注意)。 Q.E.D.
証明. よりわかる。 Q.E.D.
のときに
を判定する簡明なる公式はあるでしょうか?
butchi数環の環構造は次のように分かります:
証明. 準同型写像
を考える。これが、全射であることはの元を任意にとったときに、係数の
進展開において
を
に置き換えて得られる冪級数を考えれば確かめられる。
は自明であるが、逆に
を任意にとる。このとき、定理1より
が存在してが成り立つ。
の仮定より
であるから、を代入すれば
となって、が従う。すなわち、
が示された。よって、準同型定理により
が言える。
についても同様。 Q.E.D.
butchi氏の卒論の13ページには
「係数が整数であるようなすべての多項式を表現できるようになる。」
とあります。
は
の、
は
の数の拡張体系と思えますが、どれぐらいの大きさかというと、それぞれ整数係数多項式、
進整数係数冪級数に対応するだけあることがわかりました。
また、この同型により、および
はUFDであることが分かります。
の素イデアルは3つしかないので、
の方でbutchi既約元について考察しましょう。
を除くbutchi数は一意的にbutchi既約元分解でき、butchi自然数は一意的にbutchi素数分解できます。
において素数および既約多項式は既約元であることに注意してbutchi素数分解の例を見てみましょう:
は全てbutchi素数である。butchi数表示はそれぞれ
で与えられる。従って、例えば
や
はbutchi素数分解の例となっている。
ふと気になったことがあるので、問として書いておきます:
"星座"はTaoの論文
"The Gaussian primes contain arbitrarily shaped constellations"
にインスピレーションを得たものです。
Taoの論文の主結果がどのようなものかについてはtsujimotter氏による解説動画
www.nicovideo.jp
を参照してください。
Taoの論文における星座と上の問における星座の定義は同じにはできません。はアーベル群をなしますが、正の整数倍は相似拡大に対応しません。
作用によって相似拡大を定義するのではなく、もっと素朴に図形的に相似拡大を定義します(点の間隔を広げるのであって、点の個数は増えないことに注意)。あるいは星座の定義においてのみ群構造を入れ替えるという手もあるかもしれません。
上の問をもう少し意味が定まるように述べると
「与えられた有限サイズのドット絵と全く同じ形(相似拡大は許す)のbutchi素数が存在するのはどのような場合か?」
となります。
平行移動してしまうと必ず可約になるのでTaoのときとは様子が違います。また、全ての形を実現することは叶わないようで、例えば正方形の頂点配置は可約になってしまいます。
 次元butchi数
次元butchi数
自然と思われる拡張は次元butchi数環
を
と定義するというものです。ここで、は
進整数環で、従って
が素数であるか否かによって
が整域であるか否かが変わってくるという代数構造の違いが現れます。
次元butchi整数環も同様に定義できます。
などを考えると、butchi数表示の一意性が成り立たなくなります。
特に、次元butchi数(三次元空間内の3色ドット立体)の可視化などには興味があります。