レスターの定理

高校数学整数整数-9

じすがなぼ

まずは歌いましょう。

www.youtube.com

参考記事: 三角形の五心の覚えておくべき性質を整理 | 高校数学の美しい物語

重心

三角形 $ABC$ に対して、辺 $BC$ の中点を $M_A$ とする。辺 $CA$ , 辺 $AB$ についても同様に考えて $M_B, M_C$ を定義する。

定理: 直線 $AM_A, BM_B, CM_C$ は一点で交わる。

この一点を重心という。

特徴: 重心を $G$ とすると、 $AG:GM_A=BG:GM_B=CG:GM_C=2:1$ が成り立つ。

垂心

三角形 $ABC$ に対して、点 $A$ から辺 $BC$ への垂線の足を $H_A$ とする。辺 $CA$ , 辺 $AB$ についても同様に考えて $H_B, H_C$ を定義する。

定理: 直線 $AH_A, BH_B, CH_C$ は一点で交わる。

この一点を垂心という。

外心

三角形 $ABC$ に対して、辺 $BC$ の垂直二等分線を $l_A$ とする。辺 $CA$ , 辺 $AB$ についても同様に考えて $l_B, l_C$ を定義する。

定理: $l_A, l_B, l_C$ は一点で交わる。

この一点を外心という。

特徴: 外心は三角形 $ABC$ の外接円の中心である。

内心

三角形 $ABC$ に対して、 $\angle A$ の二等分線を $\ell_A$ とする。角 $\angle B$ , 角 $\angle C$ についても同様に考えて $\ell_B, \ell_C$ を定義する。

定理: $\ell_A, \ell_B, \ell_C$ は一点で交わる。

この一点を内心という。

特徴: 内心は三角形 $ABC$ の内接円の中心である。

傍心

三角形 $ABC$ に対して、 $\angle A$ の二等分線を $\ell_A$ とする。また、角 $B$ の外角、角 $C$ の外角の二等分線をそれぞれ $\ell'_B, \ell'_C$ とする。

定理: $\ell_A, \ell'_B, \ell'_C$ は一点で交わる。

$B, C$ についても同様に考えることによって得られる三角形 $ABC$ の外側の三つの点を傍心という(つまり、傍心は三つある)。

特徴: 定理で定まる点は辺 $BC$ , 直線 $AB$ , 直線 $AC$ に接する円(傍接円)の中心である。

第一Fermat-Torricelli点

三角形 $ABC$ に対して、 $BC$ を一辺とする二つの正三角形のうち直線 $BC$ について点 $A$ と反対側にあるものを $\Gamma_A$ とする。辺 $CA$ , 辺 $AB$ についても同様に考えて $\Gamma_B, \Gamma_C$ を定義する。

定理: $\Gamma_A$ の外接円と $\Gamma_B$ の外接円と $\Gamma_C$ の外接円は一点で交わる。

この一点を第一Fermat-Torricelli点という。

特徴: 三角形 $ABC$ が内角が $120^{\circ}$ 以上の頂点を持たないとき、第一Fermat-Torricelli点 $F$ は三頂点からの距離の和が最小となるような点になっている。また、 $\angle AFB=\angle BFC = \angle CFA=120^{\circ}$ になっている。

参考記事: 三角形のフェルマー点の3通りの証明 | 高校数学の美しい物語

第二Fermat-Torricelli点

三角形 $ABC$ に対して、 $BC$ を一辺とする二つの正三角形のうち直線 $BC$ について点 $A$ と同じ側にあるものを $\Delta_A$ とする。辺 $CA$ , 辺 $AB$ についても同様に考えて $\Delta_B, \Delta_C$ を定義する。

定理: $\Delta_A$ の外接円と $\Delta_B$ の外接円と $\Delta_C$ の外接円は一点で交わる。

この一点を第二Fermat-Torricelli点という。

参考記事: 三角形の五心の話(10)Fermat点

Napoléonの三角形とNapoléon点

第一・第二Fermat-Torricelli点の記号を利用する。

定理: $\Gamma_A, \Gamma_B, \Gamma_C$ の重心をそれぞれ結んでできる三角形は正三角形である。また、 $\Delta_A, \Delta_B, \Delta_C$ の重心をそれぞれ結んでできる三角形も正三角形である。これら二つの正三角形の重心は三角形 $ABC$ の重心と一致する。

これらの正三角形をそれぞれNapoléonの外三角形・内三角形という。

定理: $\Gamma_A, \Gamma_B, \Gamma_C$ の重心をそれぞれ $G_{\Gamma_A}, G_{\Gamma_B}, G_{\Gamma_C}$ とする。このとき、直線 $AG_{\Gamma_A}, BG_{\Gamma_B}, CG_{\Gamma_C}$ は一点で交わる。

この一点を第一Napoléon点という。

定理: $\Delta_A, \Delta_B, \Delta_C$ の重心をそれぞれ $G_{\Delta_A}, G_{\Delta_B}, G_{\Delta_C}$ とする。このとき、直線 $AG_{\Delta_A}, BG_{\Delta_B}, CG_{\Delta_C}$ は一点で交わる。

この一点を第二Napoléon点という。

参考記事: ナポレオンの定理とナポレオン点

cf. モーリーの定理 - INTEGERS

Euler線

三角形 $ABC$ の重心・垂心・外心をそれぞれを $G, H, O$ とする。

定理: $G, H, O$ は同一直線上に存在する。

$\triangle{ABC}$ が正三角形でないとき、この直線をEuler線という。

特徴: $2OG=GH, 3OG=OH$ が成り立つ。

参考記事: オイラー線の３通りの証明 | 高校数学の美しい物語

九点円

三角形 $ABC$ に対して、重心・垂心の項目で定義した点 $M_A, M_B, M_C, H_A, H_B, H_C$ を考え、 $H$ を垂心とする。 $HA, HB, HC$ の中点ををそれぞれ $D_A, D_B, D_C$ とする。

定理: 九点 $M_A, M_B, M_C, H_A, H_B, H_C, D_A, D_B, D_C$ は同一円周上に存在する。

この円を九点円という。

特徴: 九点円の中心はEuler線上にあり、外心と垂心の中点である。

参考記事: 九点円の定理の証明と諸性質 | 高校数学の美しい物語

Feuerbachの定理

定理: 三角形の内接円と九点円は内接し、傍接円と九点円は外接する。

沢(澤)山勇三郎はこの定理の証明を二十二通り与えたらしい。

参考記事: フォイエルバッハの定理と計算による証明 | 高校数学の美しい物語

Lesterの定理

定理 (Lester, 1996) 不等辺三角形の外心・第一Fermat-Torricelli点・第二Fermat-Torricelli点・九点円の中心の四点は同一円周上に存在する。

この定理によって存在する円のことをLester円という。要は次のようになっているということだ：

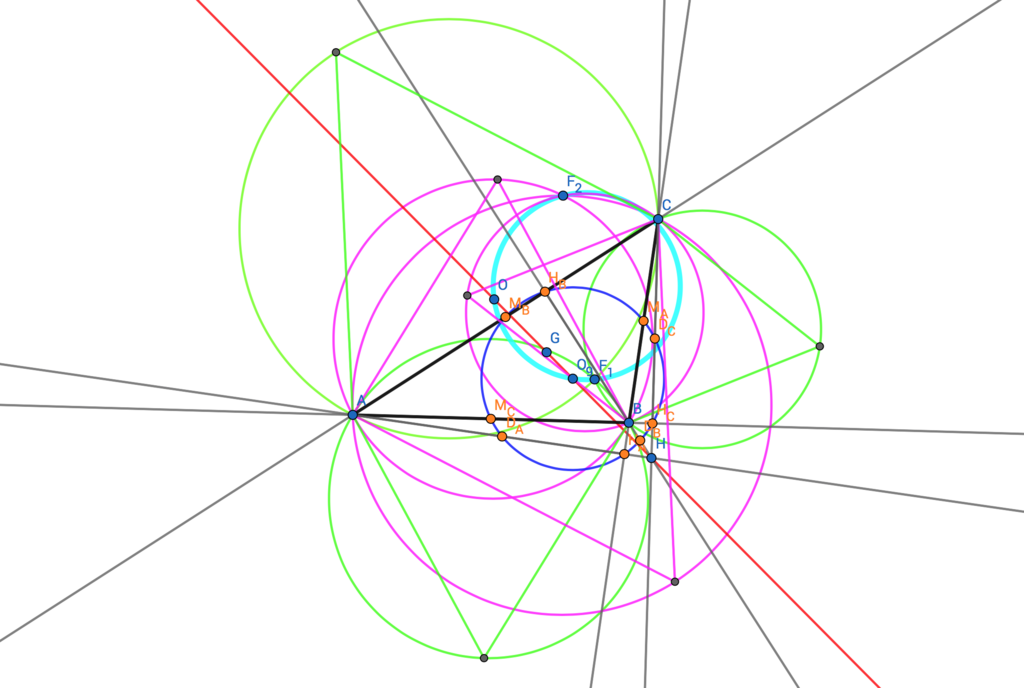
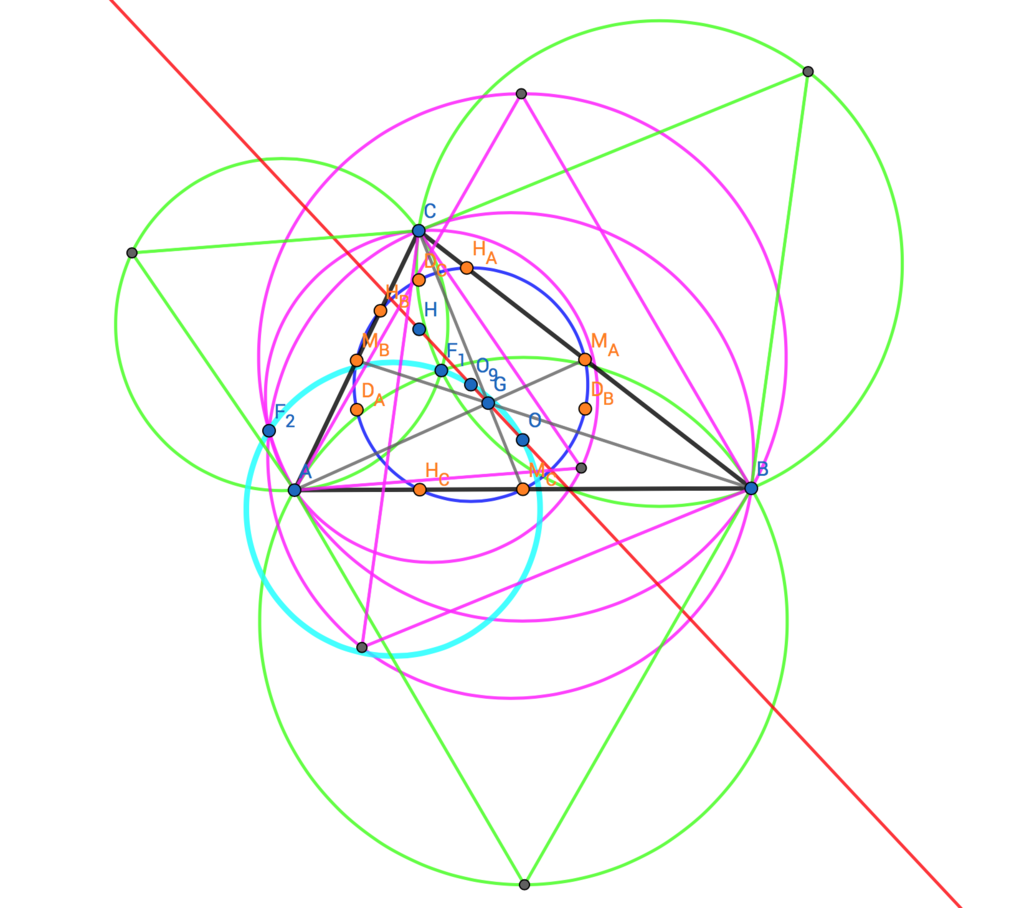
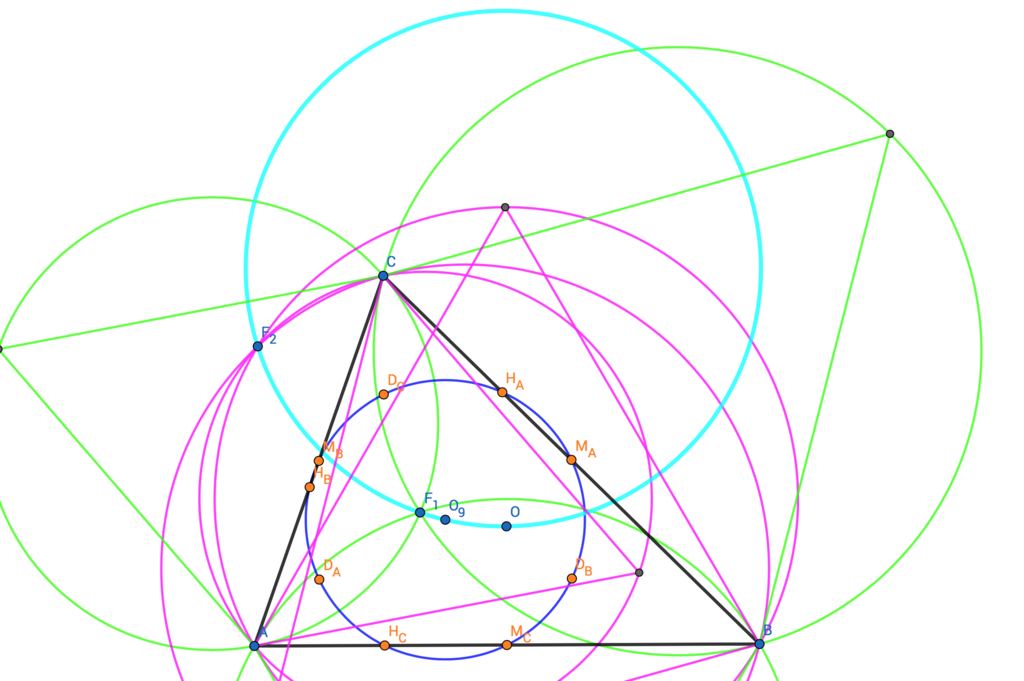
この記事ではN. I. BeluhovによるLesterの定理の証明を紹介する。

Beluhovの補題

補題 $AB \neq AC$ であるような三角形 $ABC$ を考える。直線 $AC$ に関して点 $B$ と対称な点を $P$ , 直線 $AB$ に関して点 $C$ と対称な点を $Q$ とする。三角形 $APQ$ の外接円の $A$ での接線と直線 $PQ$ の交点を $T$ とし、 $A$ に関して $T$ と対称な点を $U$ とする。このとき、 $U$ は直線 $BC$ 上にある。

$AB=AC$ だと $T$ が存在しない。

f:id:integers:20171102183546p:plain:w500

証明. $A$ に関して $B$ と対称な点を $K$ , $C$ と対称な点を $L$ とする。

f:id:integers:20171102185624p:plain:w500

示すべきことは $T$ が直線 $KL$ 上にあることである。理由: $A$ に関する対称変換で $B \leftrightarrow K, C \leftrightarrow L, U \leftrightarrow T$ と対応しており、直線は直線に移るため。

各点の定義から $AL=AC=AQ, \ AK=AB=AP$ が成り立つ。

また、

$\angle LAQ= 180^{\circ}-\angle QAC = 180^{\circ}-2\angle BAC=180^{\circ}-\angle BAP=\angle PAK$

と角度を追跡できる。よって、

三角形 $LAQ$ と三角形 $PAK$ は互いに相似な二等辺三角形であり、底角は $\angle BAC$ に等しい

ことがわかった。

接弦定理より三角形 $TQA$ と三角形 $TAP$ は相似である。この相似が定める変換 $f\colon \triangle{TQA} \mapsto \triangle{TAP}$ によって、点 $M$ を $M:=f^{-1}(K)$ と定義する( $TQMA$ と $TAKP$ が対応する)。このとき、

$\triangle{MQA}$ ∽ $\triangle{KAP}$ ∽ $\triangle{QAL}$

という相似があるため、 $QA=AL$ であることから

$\triangle{MQA} \equiv \triangle{QAL}$

が従う。すると、三角形 $QAL$ が二等辺三角形であることを思い出すと、二組の対辺がそれぞれ等しいので四角形 $ALQM$ は平行四辺形である。

また、

$\angle QAM= \angle APK = \angle BAC=\angle QAB$

と角度を追跡できるので、点 $M$ は直線 $AKB$ 上にあることがわかる。よって、直線 $QL$ と直線 $AK$ は平行である。

点 $N$ をベクトルの等式

$\overrightarrow{TN}=\overrightarrow{QL}=\overrightarrow{MA}$

が成り立つように導入する。すると、三辺相等によって

$\triangle{ALN} \equiv \triangle{MQT}$

が成り立つ。よって、

$\angle LAN = \angle QMT=\angle AKT$

が成り立ち、直線 $TN$ と直線 $AK$ は平行なので錯角を見ると

$\angle AKT=\angle NTK$

が得られる。三角形 $ATN$ の外接円と直線 $TK$ の交点を $L'$ とする。示すべきことは $L=L'$ である。

円周角の定理より $\angle NTK=\angle L'AN$ なので、 $\angle LAN = \angle L'AN$ .

同様に、

$\angle LNA = \angle QTM=\angle ATK$

および円周角の定理からわかる $\angle ATK = \angle L'NA$ より $\angle LNA= \angle L'NA$ を得る。

よって、一辺両端角相等より $\triangle{LAN} \equiv \triangle{L'AN}$ が成り立ち、これは $L=L'$ を示している。 Q.E.D.

第一・第二Fermat-Torricelli点とNapoléonの三角形の関係

定理第一Fermat-Torricelli点はNapoléonの内三角形の外接円上にあり、第二Fermat-Torricelli点はNapoléonの外三角形の外接円上にある。

証明. 三角形 $ABC$ を考える。第一・第二Fermat-Torricelli点の定義で使った正三角形 $\Gamma_A, \Gamma_B, \Gamma_C, \Delta_A, \Delta_B, \Delta_C$ の記号を用いる。これら六つの正三角形の重心をそれぞれ $T_A, T_B, T_C, S_A, S_B, S_C$ とする。第一Fermat-Torricelli点を $F_1$ , 第二Fermat-Torricelli点を $F_2$ とする。Napoléonの定理より $\triangle{T_AT_BT_C}$ および $\triangle{S_AS_BS_C}$ はともに正三角形である。

$\angle S_BF_1S_C=\angle S_BF_1A+\angle S_CF_1A$ と分割する。

$A, S_B, F_1, C$ は同一円周上にある。理由: 定義より $T_BA=T_BC=T_BS_B$ が成り立つので、 $A, S_B, C$ は $\Gamma_B$ の外接円上にある。よって、定義より $F_1$ もこの上にある。

よって、円周角の定理より $\angle S_BF_1A=\angle S_BCA=30^{\circ}$ .

同様に $B, S_C, F_1, A$ は同一円周上にあるので $\angle S_CF_1A=\angle S_CBA=30^{\circ}$ .

故に $\angle S_BF_1S_C=60^{\circ}=\angle S_BS_AS_C$ が成り立ち、円周角の定理の逆によって $F_1$ は三角形 $S_AS_BS_C$ の外接円上にあることがわかる。

次に、 $\angle T_BF_2T_C=\angle T_BF_2A+\angle T_CF_2A$ と分割する。

$A, T_B, F_2, C$ は同一円周上にある。理由: 定義より $S_BA=S_BC=S_BT_B$ が成り立つので、 $A, T_B, C$ は $\Delta_B$ の外接円上にある。よって、定義より $F_2$ もこの上にある。

よって、円周角の定理より $\angle T_BF_2A=\angle T_BCA=30^{\circ}$ .

同様に $B, T_C, F_2, A$ は同一円周上にあるので $\angle T_CF_2A=\angle T_CBA=30^{\circ}$ .

故に $\angle T_BF_2T_C=60^{\circ}=\angle T_BT_AT_C$ が成り立ち、円周角の定理の逆によって $F_2$ は三角形 $T_AT_BT_C$ の外接円上にあることがわかる。 Q.E.D.

Lesterの定理の証明

不等辺三角形 $ABC$ を考えて、上記定理と同じ記号を用いる。正三角形 $\triangle{T_AT_BT_C}$ および $\triangle{S_AS_BS_C}$ の重心は三角形 $ABC$ の重心 $G$ に一致する。

主張三角形 $GF_1F_2$ の外接円の $G$ における接線と直線 $F_1F_2$ の交点を $Q$ とする。このとき、点 $G$ に関して $Q$ と対称な点 $O$ は三角形 $ABC$ の外心に一致する。

主張の証明. 上述の定理および $F_1$ の定義より $S_AF_1$ は $G$ 中心の円と $T_A$ 中心の円の共通弦となっており、従って $F_1$ は直線 $GT_A$ に関する $S_A$ の対称点となっている。また、 $T_AF_2$ は $G$ 中心の円と $S_A$ 中心の円の共通弦となっており、 $F_2$ は直線 $GS_A$ に関する $T_A$ の対称点となっている*1。定義より $S_A$ と $T_A$ は互いに直線 $BC$ に関して対称な位置にあるので $GS_A \neq GT_A$ である。これより $F_1 \neq F_2$ がわかり、 $AB \neq AC$ より $G$ は直線 $S_AT_A$ 上にはなく $GS_AT_A$ は三角形をなしていることから $S_A \neq F_1, T_A \neq F_2$ および $GF_1F_2$ も三角形をなすことわかり、直線 $F_1F_2$ が三角形 $GF_1F_2$ の外接円の $G$ における接線と平行でないことがわかる。よって、三角形 $GS_AT_A$ に対してBeluhovの補題を適用することができ、帰結として $O$ は直線 $S_AT_A$ 上にあることが従う。 $\triangle{GS_BT_B}$ , $\triangle{GS_CT_C}$ に対しても同様に考えることによって $O$ は三直線 $S_AT_A, S_BT_B, S_CT_C$ の交点であることが示された。ところで、定義から $S_AT_A, S_BT_B, S_CT_C$ はそれぞれ辺 $BC, CA, AB$ の垂直二等分線である。つまり、 $O$ は三角形 $ABC$ の外心である。主張の証明終わり.

f:id:integers:20171102192912p:plain:w500

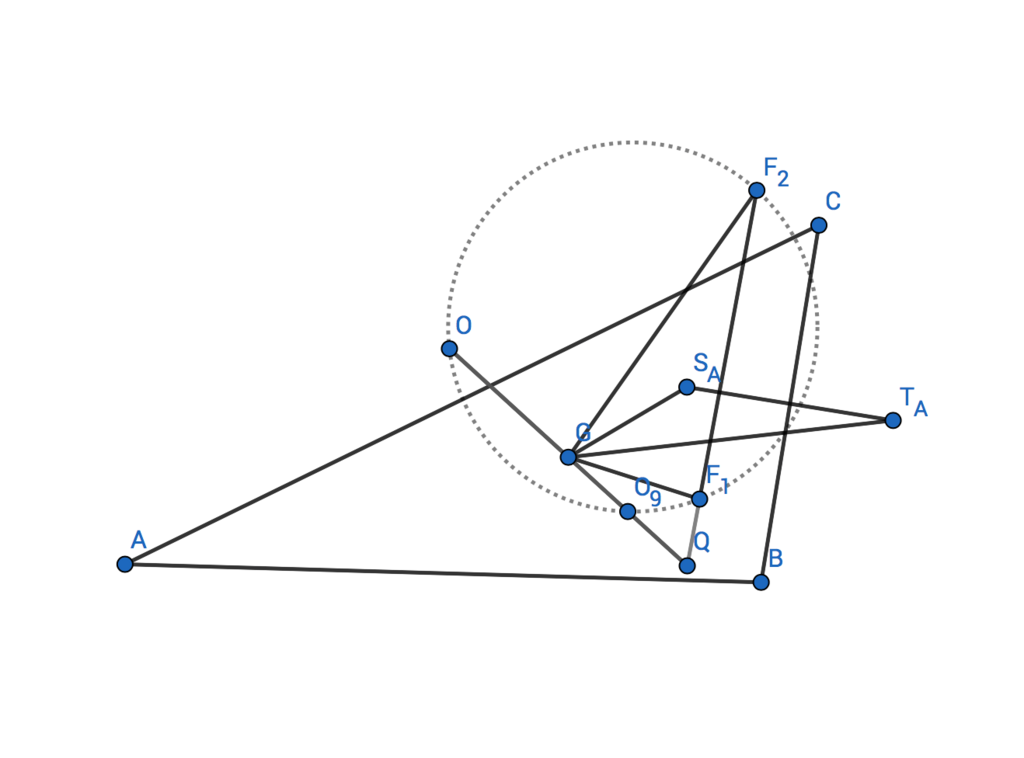
三角形 $ABC$ の九点円の中心を $O_9$ とする。三角形 $ABC$ の垂心を $H$ とすると、 $O_9$ はEuler線(=直線 $OG$ )上にあり、 $OO_9:O_9H=1:1$ , $OG:GH=1:2$ が成り立つのであった。つまり、 $OG:GO_9$ = $2:1$ であり、 $Q$ もEuler線上にあって $O_9$ は $GQ$ の中点となっている。よって、方べきの定理より