ジュリアン・ローゼン(Julian Rosen)という数学者がいます。
私は博士後期課程のとき、ジュリアンが導入したある数学的対象に着目しました。そして、彼の研究には含まれない結果を発見・証明することができ、それが私の博士論文につながりました。
その後、その対象に関する論文は幾つも現れていますが、国内で最初にそれに関する仕事をできたことは私にとって幸運でした(ジュリアンの仕事の存在自体はSさんに教えていただきいました)。
他にもジュリアンは面白い仕事をしており、私は彼の影響をとても受けています。
さて、最近になってジュリアンはまた面白い論文[R]を書いていました。それを紹介することがこの記事の目的であります。
- 数直線をティーることはできない
- 平面はティーることができる
- 数直線をティーることはできないことの証明
- 平面をティーることができることの証明(定理3への帰着)
- 平面をティーることができることの証明(定理3の証明)
- 参考文献
数直線をティーることはできない
数直線上の点の上にティー(アルファベットのT)を生やしましょう。
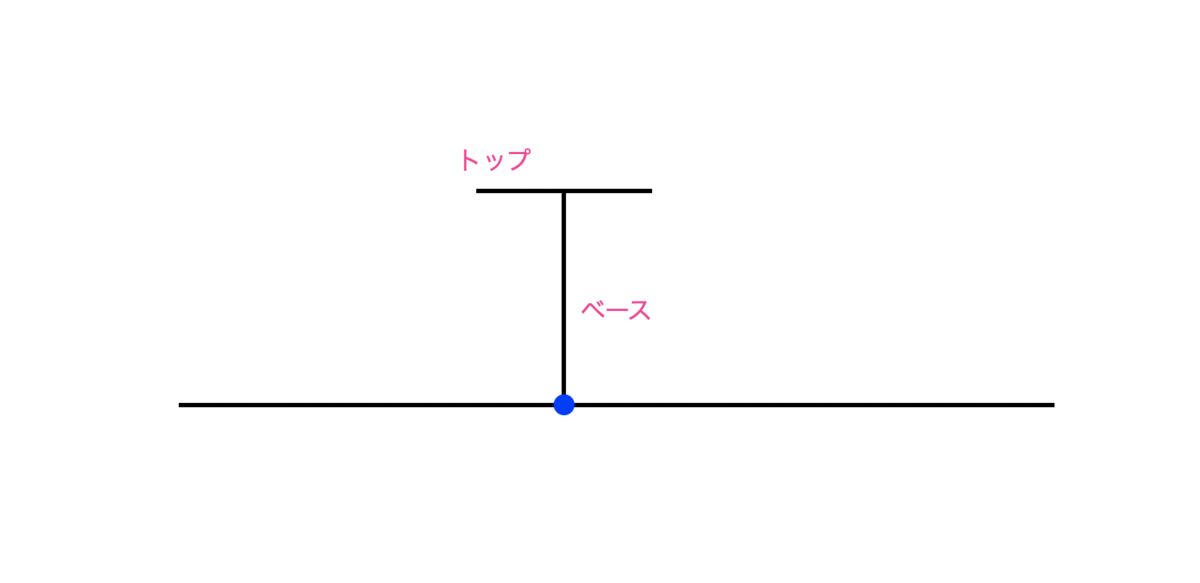
ここで、ティーとは2つの線分を合わせた(数学的には合併をとった集合を意味します)もので、1つは考えている数直線に垂直な線分で(こちらをベースとよびます)、ベースの片方の端点は数直線上にあるものとします。また、もう1つは考えている数直線と平行な線分で(よって、ベースとは垂直であり、こちらをトップとよびます)、ベースのさっきとは反対側の端点がトップの中点であるとします。
ベースとトップの長さは正の実数であればどんなものを考えてもよいものとし、特にベースとトップの長さが等しい必要はありません。
数直線上の複数の点上にティーを生やすことを考えましょう。このとき、各ティーは同一半平面上にある状況を考えることにします。
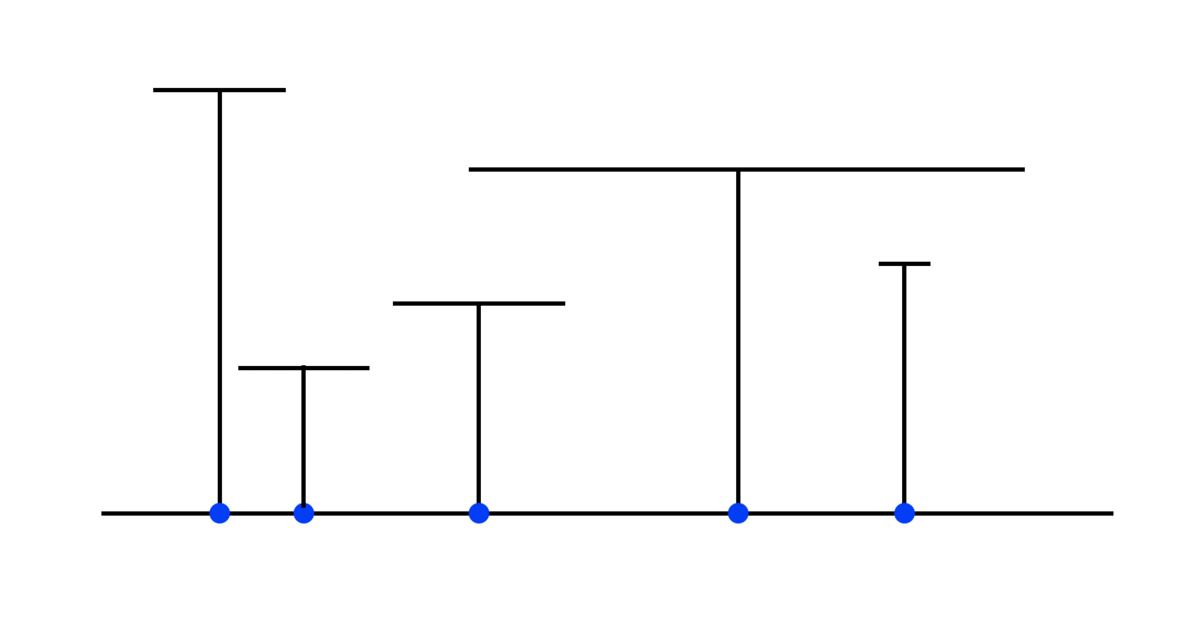
数直線の部分集合
に対して、「
をティーる」とは、「相異なる2点
に対して
上に生えているティーと
上に生えているティーが互いに交わらない(集合として共通部分が空集合となること)ように、各点
上にティーを1つずつ生やすこと」とします。
が有限集合であれば明らかにいつでもティーることができて、例えば「例1」の図は青い5つの点のなす集合を
としたときに、
をティーった例になっています。
次の図は(実際は既に見たようにティーることができるんだけれども)ティーることに失敗した例です。
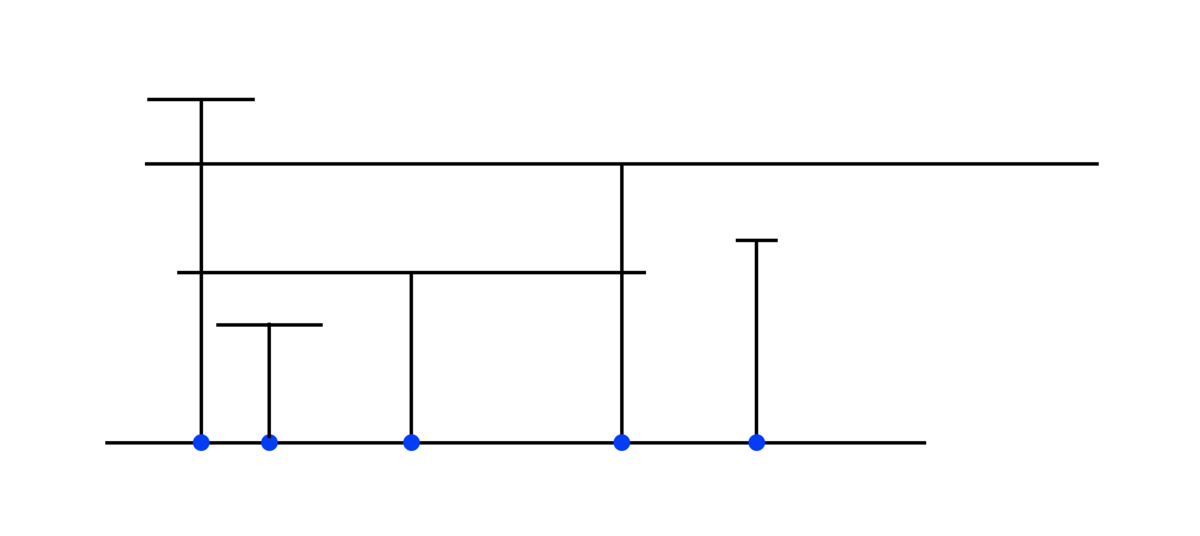
ここで問いたいことは「数直線はティーることができるか?」というものです。
次が答えです。
平面はティーることができる
前節の問題の2次元版を考えてみましょう。つまり、平面上の点の上にティーを生やします。
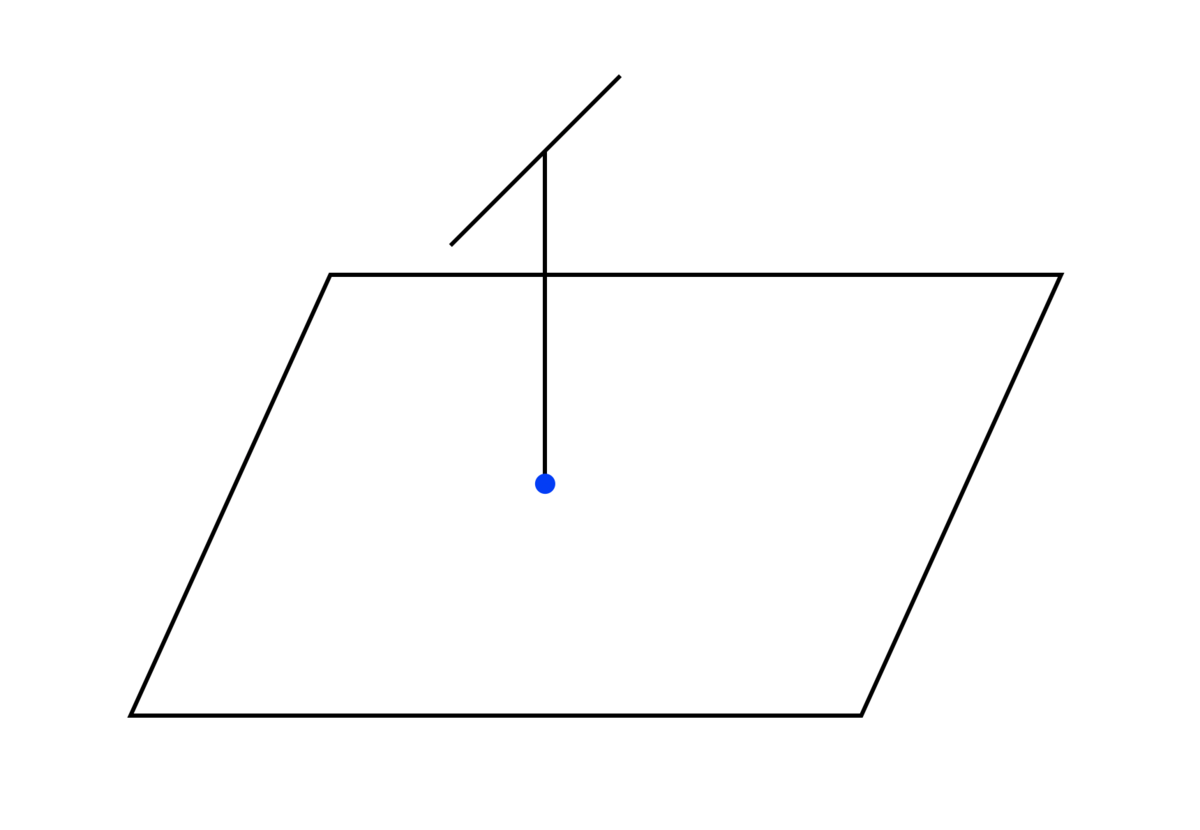
ティーは2つの線分を合わせたもので、1つは考えている平面に垂直な線分で(ベース)、ベースの片方の端点は平面上にあるものとします。また、もう1つはベースと垂直な線分で(トップ)、ベースのさっきとは反対側の端点がトップの中点であるとします。
1次元のときとの違いは、トップは考えている平面と平行な線分ですが、色々な向きを考えることができます。
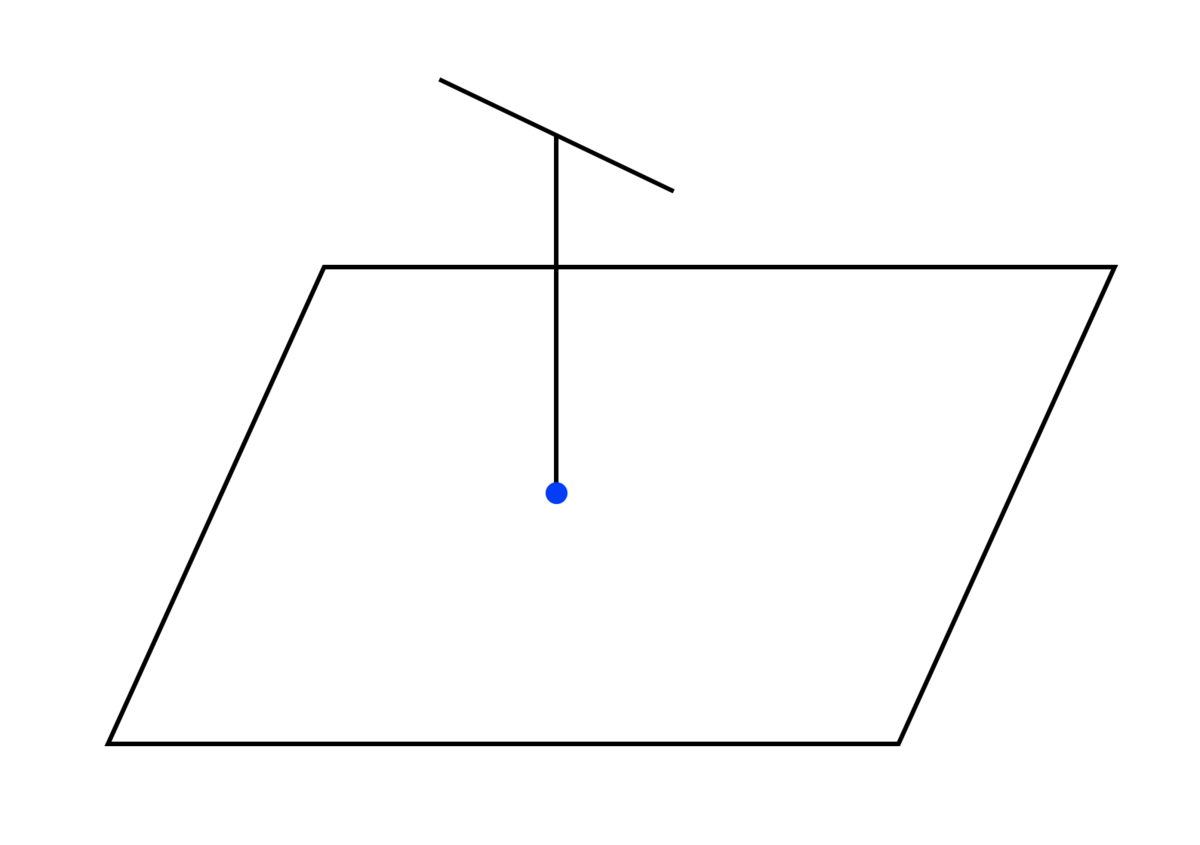
平面上の複数の点上にティーを生やすことを考えましょう。このとき、各ティーは同一半空間上にある状況を考えることにします。

平面の部分集合
に対して、「
をティーる」とは、1次元のときと同様に、「相異なる2点
に対して
上に生えているティーと
上に生えているティーが互いに交わらないように、各点
上にティーを1つずつ生やすこと」とします。
数直線はティーることができませんでしたが、平面
もティーることはできないのでしょうか?
ジュリアンは次を証明しました。
数直線をティーることはできないことの証明
この節では定理1を証明します。
を
の部分集合とし、
をティーることができたと仮定します。このとき、
は高々可算であることを示しましょう。そのことが示されれば、もちろん
はティーることができないとわかります。
をティーった際の各
上に生えているティーを
と表すことにします。
そして、各 に対して、
のトップを数直線上に射影した線分上の有理数
を、
を満たすように1組選びます(
は開区間の記号です)。
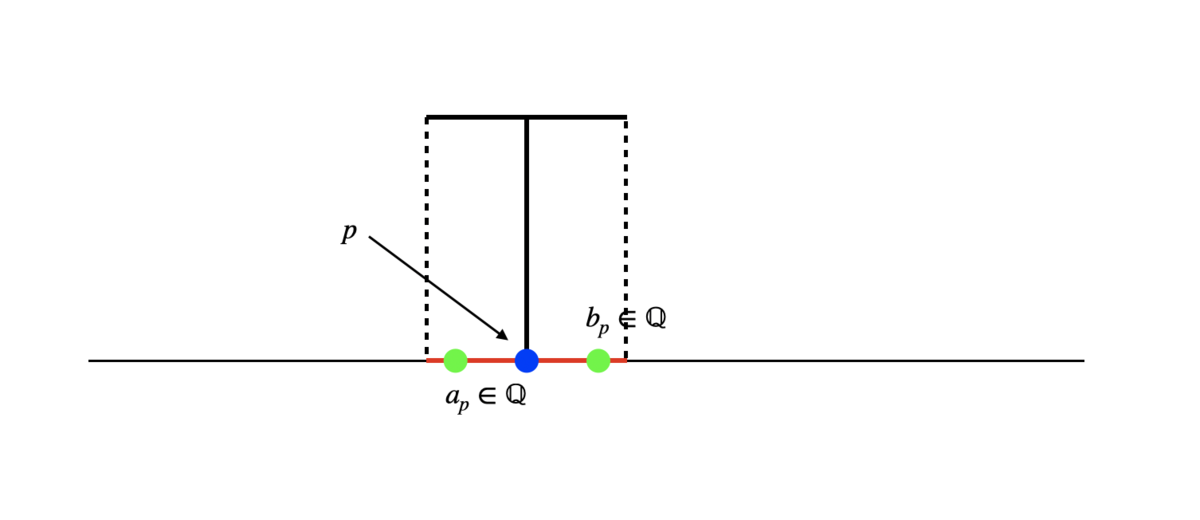
ここで、写像 を
で定義しましょう*1(
はギリシア文字の「イオタ」です)。
写像が単射であれば証明完了です。というのも、集合の濃度を絶対値記号で表すことにすると、
が得られ、
は高々可算ということになるからです。
が単射であることを示すために、相異なる2点
(
と大小関係を付けておきます)が存在して、
が成り立つ状況があると仮定しましょう(背理法による証明)。
このとき、,
とおくと、図のような状況になって、
と
は必ず交わることがわかります。

ポイントはのトップと
のトップはともに赤い線分は含むだけ長くないといけないことです。図では
のベースが
のベースより長くなっていますが、他のケースでも変わりません。
というわけで、今はをティーっていたわけですから
のはずで、これは矛盾です。よって、
は単射であり、その結果、定理1が証明されました。
平面をティーることができることの証明(定理3への帰着)
ジュリアンによる定理2の証明は次の定理3に基づきます。
- 直線
は
を通る。
が
を満たすならば、
かつ
である。
が
および
を満たすならば、
である。
ただし、は「
かつ
」を意味するものとする。
この定理3で存在する および
を用いれば、以下に説明するように
をティーることができます。むしろ、定理2より強く、ティーる際の各点上のティーのトップの長さは好きに選んでよいことまで証明できます。
一方で、定理3の証明は整列可能定理および(それと同値な)ツォルンの補題(これらは選択公理と同値です)を用いる非構成的な証明であり、従って、をティーる方法も非構成的となります*3。
定理3の証明は次の節にまわして、ここでは一旦成立を認めることにしましょう。
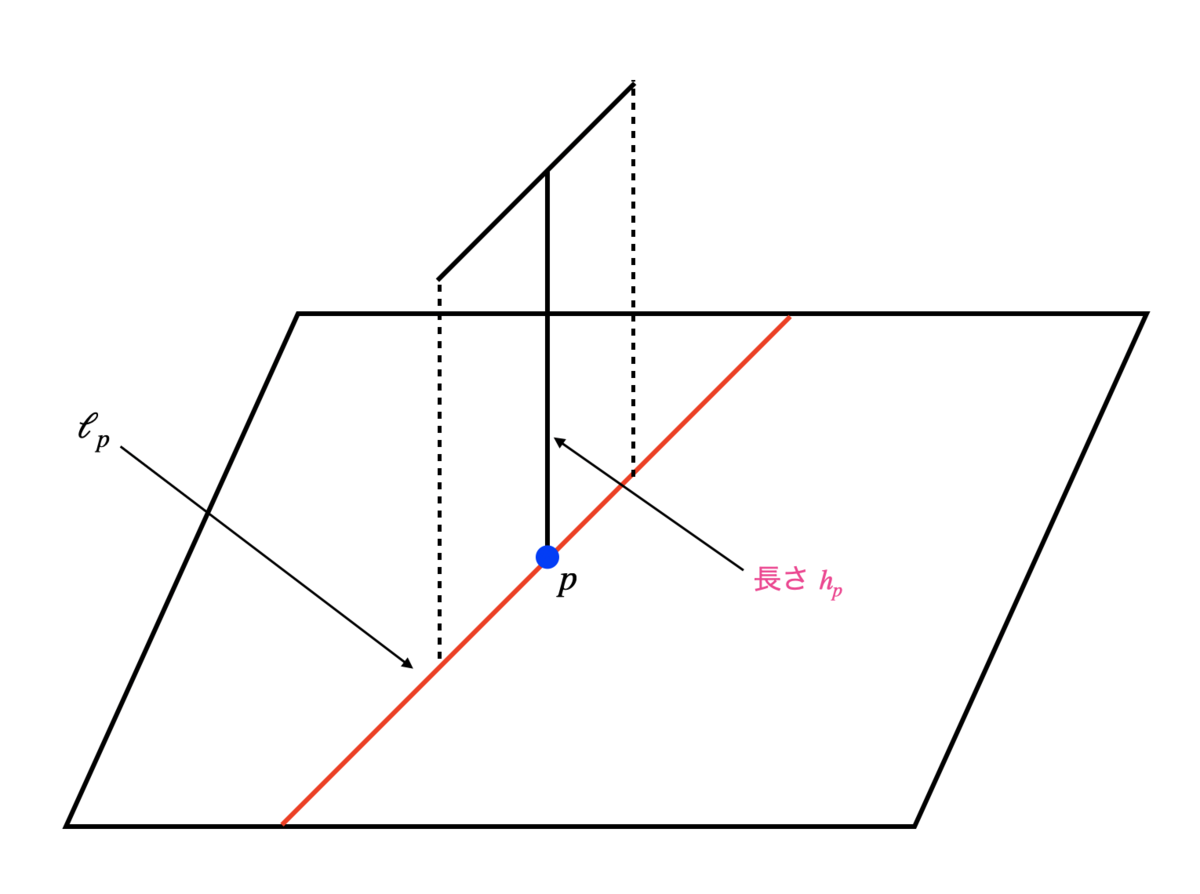
各点 に対して、
上にティー
を次のように生やします(
,
でそれぞれ
のベースおよびトップを表すことにします):
は長さ
。
は平面への射影が直線
に含まれるようなものであり、長さはあなたの好きな正の実数。
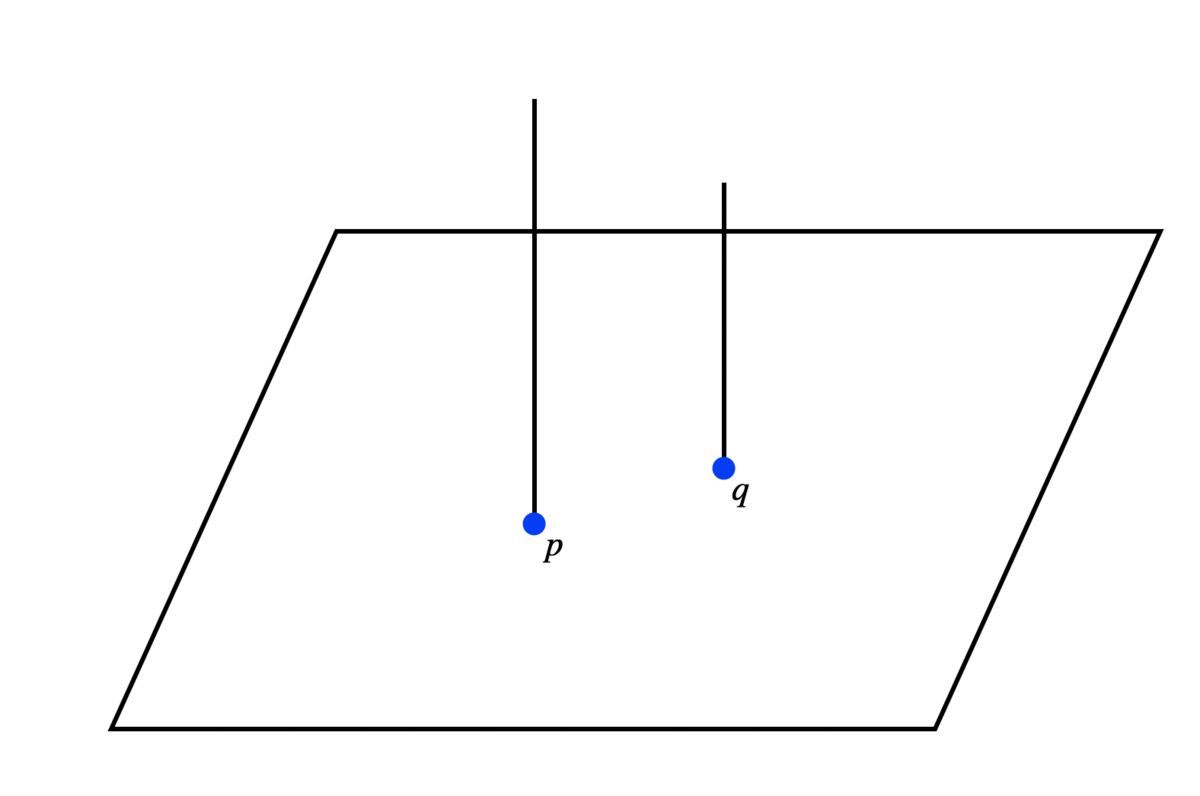
この構成でをティーることができています。それを確かめるには、相異なる2点
を任意にとって、
を示せばよいです。そのためには、
なので、
を示せばよいです*4。
が整列順序(特に全順序)であることから、
と仮定しても一般性を失いません。
また、は明らかです。
今、定理3によって なので、
がわかります。
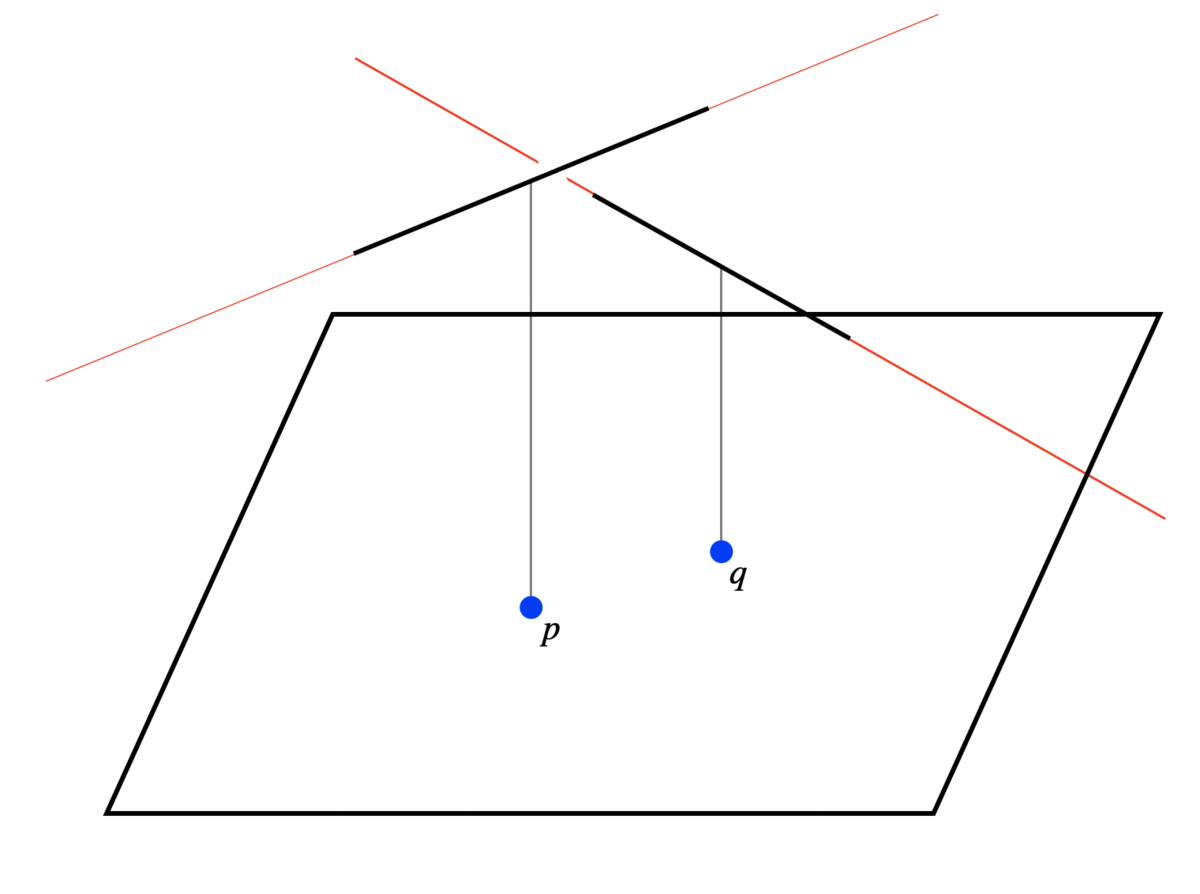
また、なので、
がわかります。
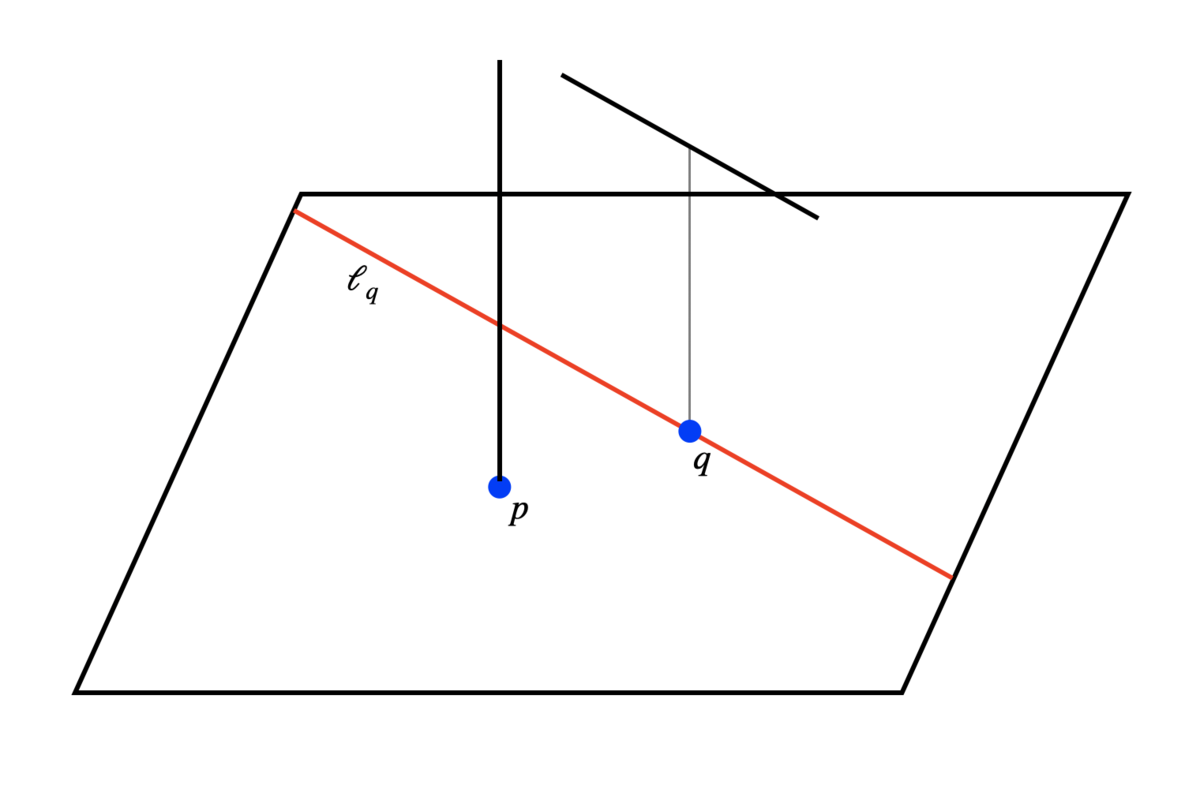
今の設定で、か
かはわかりませんが、場合分けをしましょう。
であれば直前の議論と同様に
がわかります。よって、
の場合を考えましょう。
このとき、定理3によって が成り立ちますので、やはり
が成り立ちます(もし
なら交わるかもしれません)。
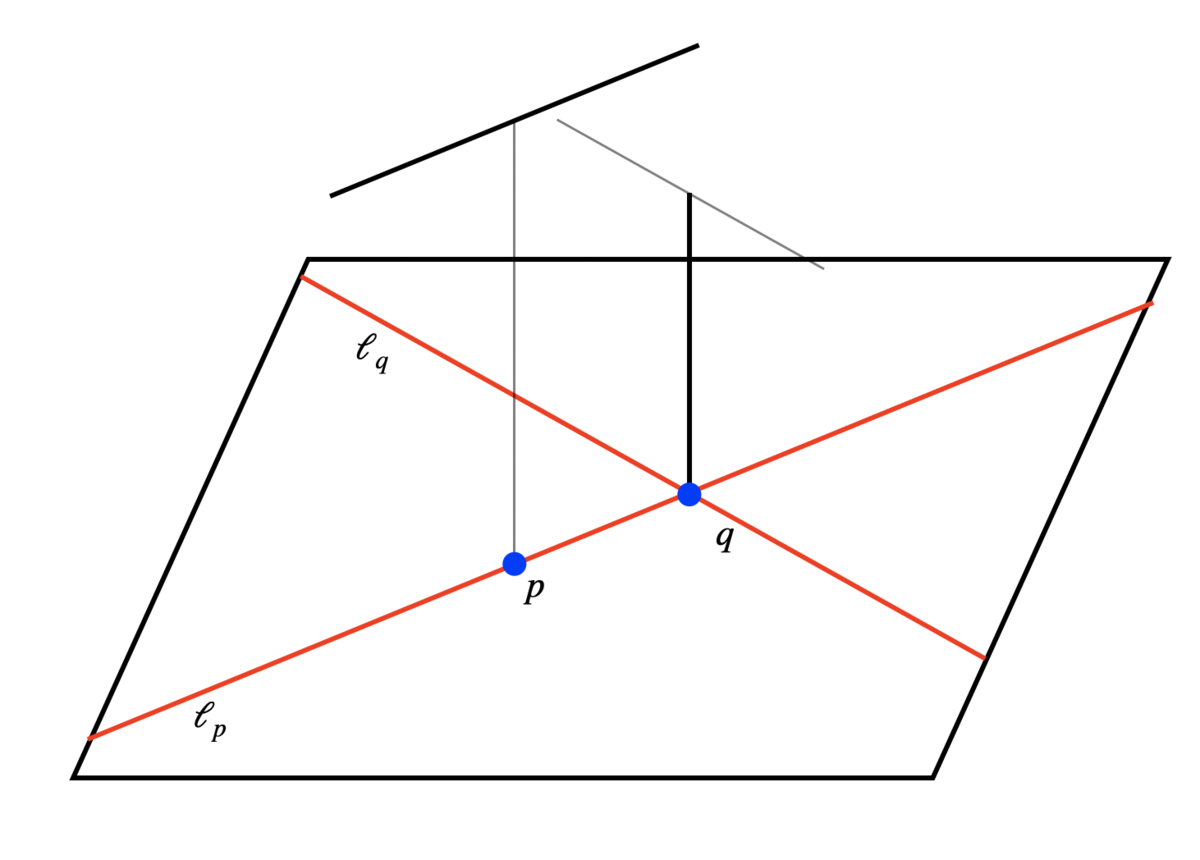
これで示すべきだったことが全て確認できました。
平面をティーることができることの証明(定理3の証明)
定理2の証明を完了させるためには、定理3の証明が残っています。適切な上の整列順序の存在を示す必要がありますが、とりあえず何かしらの
上の整列順序が存在することは次の定理からわかります。
ですが、今回の証明では何でもよいわけではありません。
集合論から必要な知識を幾つか思い出しながら議論していきます。
上の整列順序に事実2によって対応する順序数全体のなすクラスを
とします。このとき、整列可能定理によって
は空ではありません。よって、事実3によって
は最小元を持ちます。その最小の順序数に対応する
上の整列順序を
と表すことにします。
このように順序を選ぶ理由は、次の補題を使いたいからです。
補題の証明. 背理法によって証明するために、の切片
に対して
を仮定する。このとき、ベルンシュタインの定理および事実1から
が成り立つ。これは整列集合
と順序同型な
上の整列順序の存在を示す。
整列集合に事実2によって対応する順序数を
とするとき、
と
の間の順序同型によって
に対応する
の切片を
とすると、順序数の性質*10から
となって、
は
より小さい。一方、背理法の仮定から
は
に属するので、
の最小性に反する。 Q. E. D.
それでは適切な整列順序は定まったため、定理3で要求される および
の存在性を示しましょう。それはある順序集合を定義し、その集合にツォルンの補題を適用して、存在する極大元から手に入れるという形で実行されます。
集合を次のように定義します。
少しみにくいですが、集合と集合
のペアであって、以下の1.から5.の条件を満たすもの全体の集合です。
は
の切片または
。
- 任意の
に対して、
は正の実数であり、
は
を通る直線。
,
ならば
かつ
。
,
かつ
ならば
。
- 任意の
に対して、
が成り立つ。
また、上の半順序をペア
のそれぞれの成分についての包含関係によって定めます*11。
なお、には自明な元
が属することはすぐにわかります*12。
ここでツォルンの補題を思い出しましょう。
先ほどの半順序により順序集合とみたはツォルンの補題の条件を満たします。
よって、ツォルンの補題によっては極大元を持ち、それを1つとって、改めて
と表すことにしましょう。
主張の証明. を仮定すると、
は
の切片である。このとき、
が存在して、
が成り立つ。以下、
が満たされるような,
が存在することを論証したい。それが言えれば、
の極大性に矛盾し、背理法によって
が従うのだ。
を通る
内の直線全体の集合を
と表し、その部分集合を
と定める。すると、が成り立つ*14。また、
を無限集合と仮定して、事実1より
が成り立つ*15。
よって、事実1および補題よりと評価できる。
一方、が成り立つ(直線を
内で考えているから!)。従って、
は空集合ではなく、そこに属する元を1つとって、
と定める。
が有限集合のときも
となったりするだけで全く同様に
を選べる。
に対する5.より
であるため、
が空集合でない場合は通常の大小関係に関する最小元が存在する(
としよう)。
(この集合の濃度は補題より
より真に小さい)に属さない正の実数であって、
より小さいものを1つ選んで
とせよ。
が存在しない場合(先の集合が空集合の場合)は単に
に属さない正の実数であればよい*16。
これで,
が選べたので、後は
に対して1.から5.の条件が満たされていることを確認すればよい。
1.のチェック。が
でなければ、
は空集合でないので、整列性から最小元
をもつ。このとき、
が成り立つ。
2.のチェック。は正の実数としてとったし、
も
を通る直線としてとった。
3.のチェック。(
)に対して、
かつ
であればよい。これは、
および
から従う。
4.のチェック。(
)かつ
のときに、
であればよい。
が空集合であれば自明であるし、空集合でなければ、
となるようにとったのであった。
5.のチェック。任意のに対して、
を示したい。
または
の場合は
が成り立つので、
に対する5.から従う。
かつ
の場合、
なので、
が高々1元集合であることを示せばよい。もし、
で、
が成り立つならば、
となる。これは
ととっていたことに矛盾する。 Q. E. D.
以上で主張が示されたため、が得られました。このとき、
および
は定理3の条件を満たしています(大事なのは3.と4.です)。
というわけで、定理3の証明が完了した結果、前節の議論と合わせて定理2の証明も完了しました。ジュリアンの論文においては、であればいつでも
をティーることができるということが書かれています(証明は同じです)。他にもヴィーることやオーることについての言及があります。
参考文献
J. Rosen, How to tee a hyperplane, Amer. Math. Monthly 129, 781−784.
*1:ここのは開区間の記号ではなく、直積集合の元(順序対)としての記号です。
*2:任意の空でない部分集合が最小元を持つような順序を整列順序といいます。任意の2元部分集合も最小元を持つことから、整列順序は必ず全順序です。
*3:タイトルの「ジュリアンの森」はをティーった姿(数学的にはティーの族
)のことを指しているつもりですが、ジュリアンの森は存在するのですが、具体的にどのようなものであるかはこの証明からはわかりません。
*4:だからです。
*5:ここでは既に選択公理は仮定されていることに注意しておきます。
*6:順序集合であって、付随する順序が整列順序になっているもののこと。
*7:定義は割愛します(が非反射的な整列順序であるような推移的集合)。
*8:順序数,
の大小関係は
で定まります。
*9:一般の整列集合に対しても全く同様に切片が定義できます。
*10:.
*11:つまり、2つのペアを,
と略記するとき、関係
を
かつ
によって定めます。
*12:整列集合には最小限が存在するので、それを
とおけば、
がわかります。つまり、空集合は
の切片です。
*13:本当は「ペア」と言うべき。以下も同様の省略表現を用いる。
*14:から
への写像を直線
の像を
に属する何かしらの元として定めると、これは単射である。
*15:から
への写像を直線
の像を
および
,
を満たす
(何かしら1組とる)として定めると、
に対する条件3.から
なので特に
であり、よって、
は
と
の交点(それは
ではない)からなる1元集合である。よって、この写像は単射である(
とそれ以外の点を結ぶ直線は1つしか存在しない)。
*16:定理3には5.に対応する条件が現れていないですが、実のところ、5.はここでをとる際に
が有限集合であって欲しいために用意された条件だと思います(空でない有限集合は必ず最小元を持つ)。ただ、5.で考える集合が高々1元集合であると要請することは一般には不可能なことがわかりますので、高々2元集合としているのだと思います。