この記事は素数大富豪Advent Calendarの16日目の記事です。
adventar.org
おかげさまで私が考案したトランプゲーム『素数大富豪』は忘れ去られることなく、今もプレイヤーを増やし続けながら盛り上がっていると実感します。素数大富豪を愛する皆様に本当に感謝しています。
素数大富豪の研究が進むと色々と見えてくることがあり、例えば先手がかなり有利なゲームのようです。そこで、マモさんは先手有利を軽減するための遊び方を提言してくださっております。
先手有利を軽減するプレイ方法の紹介 - まもめも
他にも、ルール自体をある程度変更した素数大富豪で遊ぶことを提言してくださっている方もおられます。ruia_primeさんのb進素数大富豪やicqk3さんのガウス素数大富豪などがあります。
この記事では私も新しい素数大富豪の遊び方を一つ提案しようと思います。その名も『限定素数大富豪』。
発想の経緯
オリジナルの素数大富豪の発想の経緯は
integers.hatenablog.com
に書きました。また、最近になって梟老堂 さんの『素数大富豪Lv. 0』が販売されました。
まずはこれらのゲームの分析を行いたいと思います。
素数大富豪は大富豪をベースとして考案されたゲームですが、出来上がったゲームはゲーム進行の型に限っても大富豪とは異なる要素を幾つか含んでいます(山札の存在や複数枚出しにおける十進法読みなど)。このようなゲームの型に基づいたゲームを『素数大富豪型ゲーム』と呼ぶことにしましょう。つまり、『素数大富豪型ゲーム』というトランプゲームの分類を新たに作り、素数大富豪と素数大富豪Lv. 0はともに素数大富豪型ゲームに属すというわけです。
素数大富豪は『素数大富豪型ゲーム』であって、更に『素数の暗記・博打要素』を持ったゲームとなっています。これは『素数コレクター』になるという新しい楽しみも生み出しました。大きい素数を知っているほどゲームに有利になるため、暗記が得意な人や素数大富豪で勝てるようになりたい人はどんどん大きい素数を覚えていっており、大会上位のプレイヤーは既に7枚出し以上を標準装備しつつあります(素数の暗記要素)。また、必ずしも勝つことにはこだわらないが、大きい素数と出会い、面白い語呂合わせを発見することを喜びとするような人々も現れました(素数の博打(=出会い)要素)。
一方で、暗記は基本的にはゲーム中に行うことではないため、(手札の引きが運なのは大富豪型である以上仕方ないですが、与えられた手札を用いてどういう戦略を取るかという)純粋な頭脳戦として遊ぼうと思ったときにたくさん暗記している人とそうでない人の間に大きな格差が生まれてしまいます。 チェックなどの特殊な戦略があってそれはそれで面白いのですが、暗記格差が大きいとあまり有効ではありません。この辺の悩みはもりしーさんの記事にも書かれています。(多くの人間がそうだと思いますが)暗記が苦手な人にとっては、たとえ戦略を立てるのが上手であったとしても、素数大富豪はあまり強くなれないゲームとなってしまいます。
チェックなどの特殊な戦略があってそれはそれで面白いのですが、暗記格差が大きいとあまり有効ではありません。この辺の悩みはもりしーさんの記事にも書かれています。(多くの人間がそうだと思いますが)暗記が苦手な人にとっては、たとえ戦略を立てるのが上手であったとしても、素数大富豪はあまり強くなれないゲームとなってしまいます。
このようなある種のデメリットがありながら、素数大富豪のルールをこのようにデザインした理由は『ゲームで扱える素数の個数』が非常に多いことに多大なる魅力を感じたためです。素数好きとしてこの点で素数大富豪のルールに満足し、ゲーム性におけるデメリットの排除は必要に応じて素数大富豪の派生を作っていただければよいと判断しました。
素数大富豪Lv. 0はそうして作られた派生ゲームと見ることができます。『素数大富豪型ゲーム』でありながら、プレイヤー間格差を少なくするために『素数の暗記・博打要素』を著しく減らすことに成功しています。他にも素数大富豪はトランプゲームなので偶数が手札にたくさんあると初心者のうちは捌きにくいといった問題がありましたが、素数大富豪Lv. 0はカードの枚数も調整されています。また、カードデザインもとても素晴らしいです。ですが、ここでは『素数の暗記・博打要素』がどのように変更されたかをもう少し詳しく見ていきます。
『素数の暗記要素』は『ゲームで扱える素数の個数』を単純に減らすことによって実現されています。素数大富豪Lv. 0では基本的には一枚出しか二枚出ししかできず、カードの特殊効果で三枚出しを一部許しています。三枚出しができる場合も各カードが一桁でなければならないという制限を設けることによって三桁を超えることがありません(この制限がなければ三枚出しで六桁まで可能になってしまう)。ちなみに素数大富豪Lv. 0で出せる最大の素数は です。一方で、扱える素数の個数が少なくても例えば三桁の素数を全て覚えている人は多くないでしょうから暗記要素(という素数大富豪の一つの楽しさ)が完全になくなったわけではありません。
です。一方で、扱える素数の個数が少なくても例えば三桁の素数を全て覚えている人は多くないでしょうから暗記要素(という素数大富豪の一つの楽しさ)が完全になくなったわけではありません。
『素数の博打要素』は『素数の暗記要素』が減ったことによって連動して減っています。また、各カードにヒントが書いてあるので更に減ります。それでも、ヒントが奇数である場合は「右からつけるのか」・「左からつけるのか」という運要素があります。このように博打要素(という素数大富豪の一つの楽しさ)も完全になくなったわけではありません。ちなみに素数大富豪では 枚出しで間違えると
枚出しで間違えると 枚手札が増えるというペナルティがありました。エゴサなどしているとこの点についてもっといい方法があったのではという指摘をよく見ます。ペナルティといいつつ手札を増やす戦略にもなりますし、オリジナルのルールは現行のままでよいと考えていますが、初心者向けにはペナルティを一律一枚とするというケースもよくあってペナルティが少なくてもゲームは可能です。素数大富豪Lv. 0では思い切ってペナルティなしとなっています(なお、10のカードがペナルティの特殊効果を持っている)。
枚手札が増えるというペナルティがありました。エゴサなどしているとこの点についてもっといい方法があったのではという指摘をよく見ます。ペナルティといいつつ手札を増やす戦略にもなりますし、オリジナルのルールは現行のままでよいと考えていますが、初心者向けにはペナルティを一律一枚とするというケースもよくあってペナルティが少なくてもゲームは可能です。素数大富豪Lv. 0では思い切ってペナルティなしとなっています(なお、10のカードがペナルティの特殊効果を持っている)。
素数大富豪Lv. 0はこのように『素数の暗記・博打要素』を減らしたゲームになっていますが、そのことによって『素数大富豪型ゲーム』の戦略性の部分が際立っています。なので、素数大富豪の持つ独特なフレイバーを味わいつつ対戦ゲームとして十分に楽しめる仕上がりになっていると感じます。
素数大富豪Lv. 0はもちろん素数コレクターには物足りないものとなっていますが、それは『素数の暗記・博打要素』のもつデメリットを減らすために作られたゲームである以上仕方のないことですし、『Lv. 0』は初心者向けなので、そこから興味を持っていただいた方には素数大富豪を遊んでもらうというのが本来の目的の一つでもあります。
素数大富豪Lv. 0をやってみて、私は『素数大富豪型ゲーム』のもつ戦略ゲーとしての面白さを再認識しました。素数大富豪は素数を暗記したらそれで最強というわけではありません。暗記の度合いによってプレイヤー間格差は生じますが、暗記レベルが同じプライヤー同士の戦いにおいては『戦略』も非常に重要になります。というのも、与えられた手札に対して組める素数は一般にたくさんあるので、どれが最善の出し方であるかを短時間で判断するのはとても頭を使うのです。
一方で、素数大富豪Lv. 0は三枚出しまでしかできないために、素数大富豪の『素数大富豪型ゲーム』としての面白さが一部失われているとも言えます。そこで私は次のような欲求に駆られました。
『素数の暗記・博打要素』をなくし『素数大富豪型ゲーム』の戦略性を著しく際立たせた頭脳ゲームでありながら、にもかかわらず『ゲームで扱える素数の個数』は膨大である
ようなゲームを作りたい。12/10の朝にこのように思って電車の中で考えたのが『限定素数大富豪』です。副産物的ゲーム要素としてトレーディングカードゲームが持つコレクト要素やデッキ構築の楽しみのような要素があると思っています。
の円に内接する正
角形の周の長さを
とするとき、
が成り立ちます。
を円周率の近似とすることは昔からなされていて、初等幾何学的に
角形の周の長さを計算して円周率を小数第35桁まで計算したそうです。
までのデータしか与えられなくとも、残りの
(
)の値を上手く近似的に補完することによって収束を加速させる増約術を開発しました(関の使ったデータと手法では円周率を小数第18位まで求められます)。
をあらかじめ計算しておきます。これを用いて
で計算します。その数値をみると、
は
で
に収束することが強く期待されます。
以降を
と置き換えることによって
は
に収束することがみてとれ、
を矢の長さ
と直径
を用いて表すという問題を考えます。
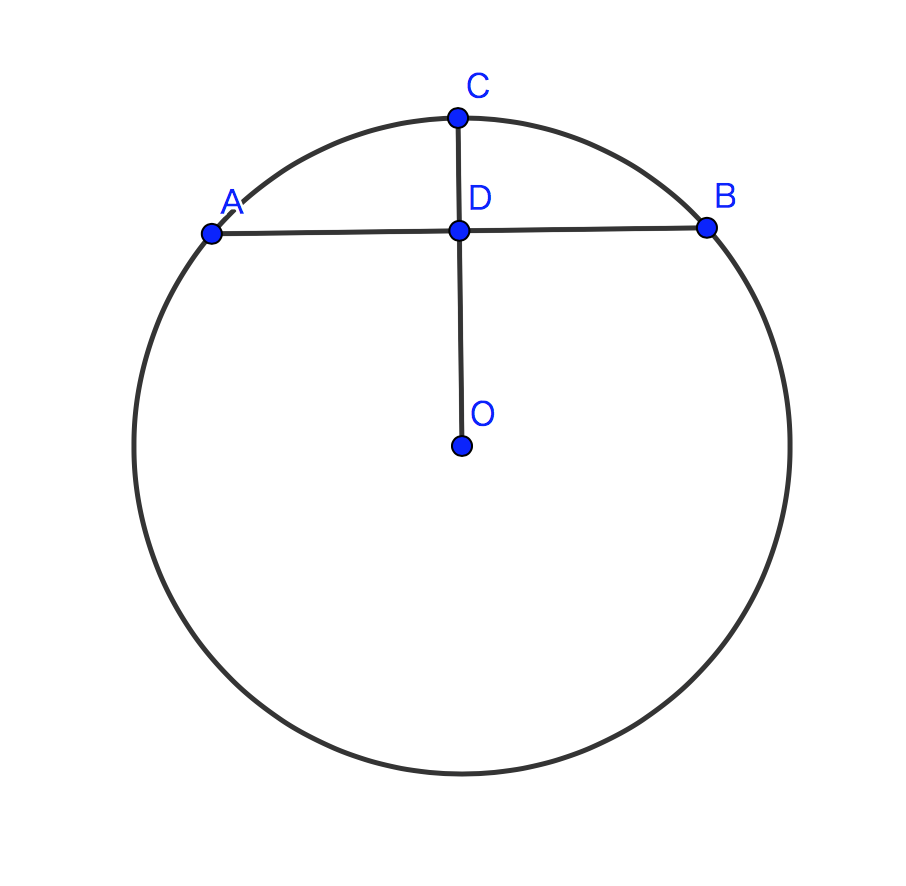
の長さを
とし、
を矢と呼んで、その長さを
としています。建部は
のときに弧
を六十四等分して、定半背冪
を累遍増約術で計算しました。その結果、
)、
を連分数展開して近似分数を求めると
が係数であろうと見当をつけます。続けて
を連分数展開して近似分数を求めると
が係数であろうと考えます。このようにして、建部は
とすると弧長の公式より
とおくことによって、建部の式は
のテイラー展開
を代入すれば

