私の推し1458次方程式は
です。
解説
沢口一之が著書『古今算法記』に出題した15題の遺題の第14問は次のような問題でした。
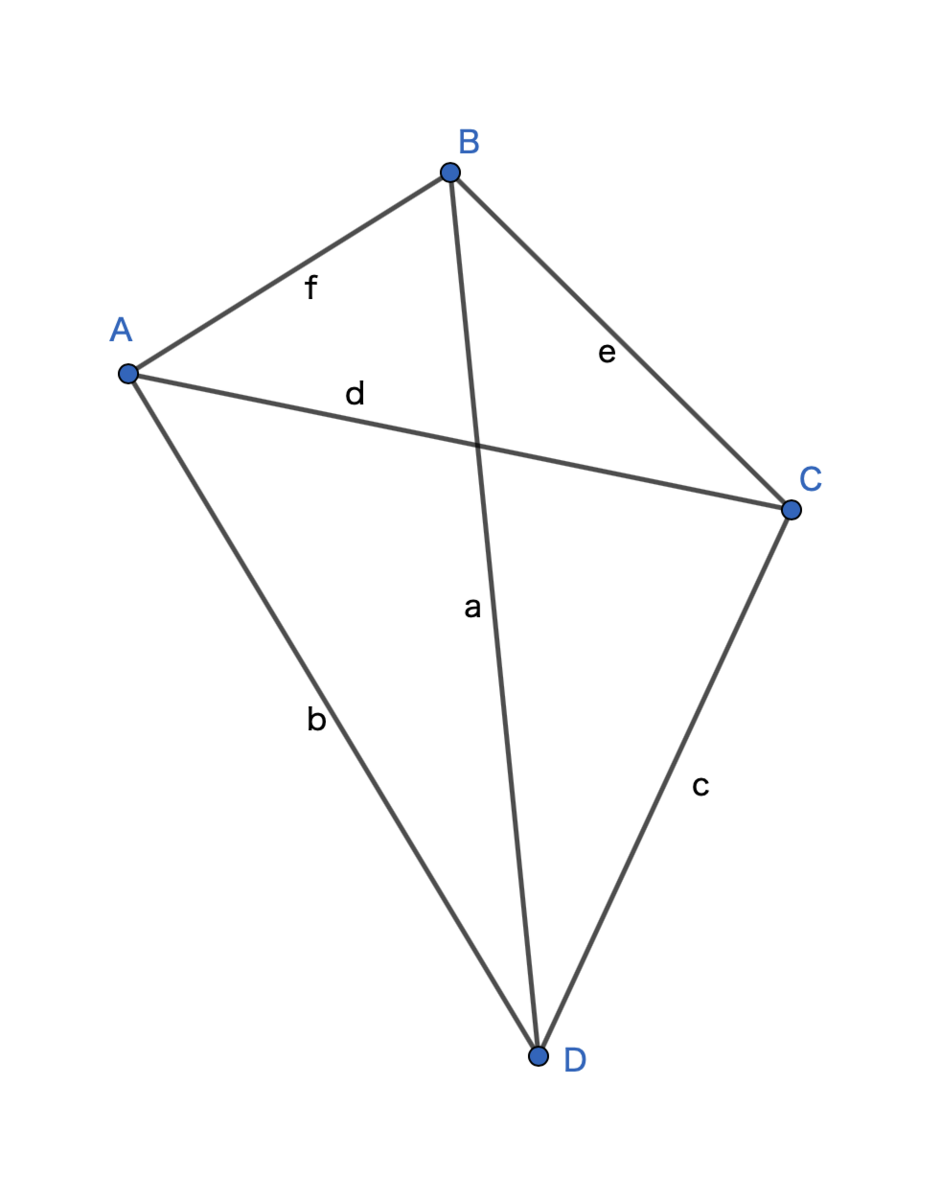第14問図図において、BD、AD、CD、AC、BC、ABの長さをそれぞれ 
とおく。以下の関係
が成り立つとき、 の値を求めよ。
関孝和は著書『発微算法』において沢口一之の問題の解答を掲載していますが、実際には特定の未知数（第14問の場合は 
）が満たす1変数代数方程式を求め、それをもって（本質的に）答え（たこと）にしています。
ただ、この第14問については「計算が多く, 文が繁雑になるので*1」方程式を得るための手順の概要と次数（= 1458次！）のみを記して、具体的な方程式は書いていません。
冒頭の方程式は、まさしく の満たす1458次方程式です！！！！
（SVG形式の画像ですので、是非拡大してみてください）
経緯
岩波書店から出版された『関孝和全集』の影響で最近、関孝和のことばかり考えているのですが、先日勉強したことを１つの記事にまとめました。
integers.hatenablog.com
関孝和が具体的には記さなかった1458次方程式を是非ともこの目で見たいとなったものの、計算が大変そうだったので、この記事の段階では一旦諦めることにしました。
その代わりに、宮城清行という人物が1712年出版の『和漢算法大成』に1458次方程式の具体形を掲載しているという情報を得、記事のタイトルに「関孝和」を入れるのを忘れるほど興奮したのでした。
ですが、具体形が掲載されていると言っても、我々が想像する1458次方程式の形では記述されていません。
例として、『発微算法』における沢口一之の第1問の答えを見てみましょう。これは最終方程式が6次方程式なのです。すると、現代的な感覚では
という形で答えが書いてあると期待します。ところが、実際の答えは次のようになっています。
答に曰く、左の術に依りて小円径を得る。
術に曰く、天元の一を立て、小円径と為す。
云へる数を加入して中円径と為す。
これを自して得る数を甲位に寄す。
（中略）
中円径四箇と小円径二箇とを列併して得る数、これをして、甲位を以て相乗し、亦た丙位を以て相乗して、亦た円周率を以て相乗して得る数、左に寄せたると相消して、開方の式を得る。
五乗の方の飜法にこれを開き、小円径を得る。
仍りて前術を推して、大、中円径を得る。
各問に合す。
[二巻]より、読み下し文を引用。
期待した答えとは全然異なりますね。実際は6次方程式を得るための手順が記されているのです。
そして、宮城清行による1458次方程式についての8ページ超の記述も、やはり上記引用と同様に手順のみが書かれています。
そういう意味では、私はまだ関孝和の1458次方程式を見たとは言えない状況だったのです。
ところで、私の横に小林祐一朗という人間がいるのですが、昨日さらっと
「そういえば、あれできたんですけど」
と私に言うんですね。
そうして、私は見たくてたまらなかった関孝和の1458次方程式を見ることができたのです。
それはもう言葉にはできないような感動を味わったのですが、是非とも読者の皆さんにも見ていただきたいということで筆を取った次第であります。
最後に『発微算法』の第14問の節の締めの文を引用して筆を置きたいと思います。
是則循々誘入之意蓋觧難問之奥妙也尤爲學者當務之要欠
関孝和『発微算法』より引用（一部漢字は現代のものに置き換えています）
これ即ち循々誘入の意、蓋し難問を解くの奥妙なり。尤も学者当に務むべきの要となす。
[二巻]より、対応する読み下し文を引用。
以上が, 理路整然と進めていく方法である. 思うに難問をつまびらかにする奥義である. これが学問に志す者のもっとも務めるべき要件である.
[一巻]より、対応する現代語訳を引用。
参考文献
[一巻] 上野健爾、小川束、小林龍彦、佐藤賢、『関孝和全集 第一巻 現代語訳』、岩波書店、2023年
[二巻] 上野健爾、小川束、小林龍彦、佐藤賢、『関孝和全集 第二巻 訓読』、岩波書店、2023年
