この記事は日曜数学会のAdvent Calendarの17日目の記事です。
数日前、日曜数学会ミニが仙台で開催されました。この記事はそこでのライトニングトークの内容に基づいています。
和算の内容を含んでいますが、私は専門家ではなく十分な文献調査をしたわけでもないため、間違いや勘違いを多く含んでいると思われます。間違いが分かり次第その都度修正致しますが、ご了承いただけますと幸いです。
建部賢弘
建部賢弘(1664-1739)は和算家であり、『綴術算経』(1722年)に円周率の累遍増約術を用いた計算が書かれています。彼の術で小数第41位まで正確に求めることができます*1。
直径の円に内接する正
角形の周の長さを
とするとき、
が成り立ちます。
を円周率の近似とすることは昔からなされていて、初等幾何学的に
という漸化式の成立がわかるため、これを利用して円周率の近似計算をすることが原理的には可能です。ルドルフは正角形の周の長さを計算して円周率を小数第35桁まで計算したそうです。
一方、関孝和はまでのデータしか与えられなくとも、残りの
(
)の値を上手く近似的に補完することによって収束を加速させる増約術を開発しました(関の使ったデータと手法では円周率を小数第18位まで求められます)。
建部は関の増約術を繰り返し適用する累遍増約術を編み出しています。まず、をあらかじめ計算しておきます。これを用いて
をで計算します。その数値をみると、
は
で
に収束することが強く期待されます。
なので、以降を
と置き換えることによって
と考えられます。これが増約術です。ここで終わらずに円周率の近似列
に対して同様の増約術を適用します。すると、は
に収束することがみてとれ、
を得ることができます。以下、同様に増約術を繰り返すことによって(累遍増約術)、円周率の近似
に到達し、正しく計算すれば円周率の小数第41位まで正確に近似します([1])。
次に、円の弧長を矢の長さ
と直径
を用いて表すという問題を考えます。
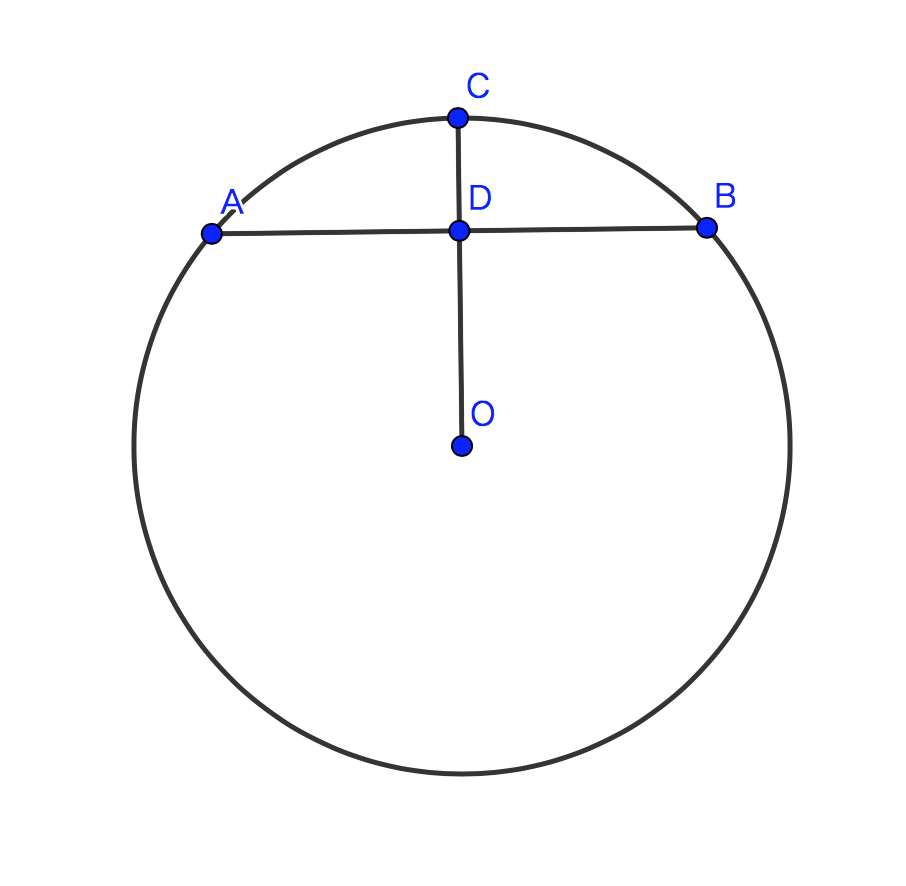
ここで、弧の長さを
とし、
を矢と呼んで、その長さを
としています。建部は
のときに弧
を六十四等分して、定半背冪
を累遍増約術で計算しました。その結果、
を得ています。建部はこれが
と級数展開されると見抜き、続く項の係数も零約術(=連分数展開)を用いることによって発見しました。例えば
として()、
を連分数展開して近似分数を求めると
となっており、が係数であろうと見当をつけます。続けて
として、を連分数展開して近似分数を求めると
となっており、が係数であろうと考えます。このようにして、建部は
なる展開を得ました*2。更に、一般には
となっていることを理解します。最後に建部は綴術によって
が
となっていることを見抜きます。そうして、建部は無限級数展開
に到達しました。
とすると弧長の公式より
であり、一方
なので、
なる関係があります。また、
なので、とおくことによって、建部の式は
のテイラー展開
に他ならないことがわかりました。この発見はEulerより15年早いとのことです。を代入すれば
が得られます。
参考文献
[1] 小川束, 円理の萌芽–建部賢弘の円周率計算–, 数理解析研究所講究録, 1019巻 (1997), 77–97.
[2] 村田全, 建部賢弘の数学とその思想, 科学図書館.
[3] 小松彦三郎, 綴術算経の異本と成立の順序, 数理解析研究所講究録, 1130巻 (2000) 229–244.