3/11にあしぃさんという方によって発信された次のツイートに1万リツイートを超える反響がありました:
twitter.com電車で数遊びをしている5才くらいの子がいる。
— あしぃ (@asi1024) 2016年3月11日
男の子「にぃ、さん、ご!」
母親「そうね、2たす3は5だね。」
男の子「なな、じゅいち、じゅーさん!」
母親「違うでしょ、16でしよ。」
男の子「じゅーなな、じゅーきゅ、にじゅーさん、にじゅーきゅ、さんじゅいち!」
ざわ、ざわ。。。
このツイートが創作でないならば、若干5歳にして素数の概念を習得している可能性の高いこの少年は将来有望です。是非、お会いして素数について熱く語り合いたいです。
さて、
男の子「にぃ、さん、ご!」
母親「そうね、たす
は
だね。」
の部分から、母親は少年が素数のことを考えているのではなく「」という計算を行っていると思い込んでいたものと考えられます。
そして、
男の子「なな、じゅいち、じゅーさん!」
母親「違うでしょ、でしよ。」
と会話が続きます。先ほどの推察からすると、であることから母親は
「違うでしょ、でしょ。」
と発言するはずです。
にもかかわらず「違うでしょ、でしょ。」と発言しています。
これについて、一つの可能性として、
と考えることが出来ます。もしそうであるならば、人は間違いを犯すとは言え、かように簡単な計算を間違えてしまう母親に一抹の不安を覚えてしまいます。
別のストーリーを考える
本当にそうだったのでしょうか?ツイートからは前後の文脈を読み取ることは出来ないですが、はなから「母親が計算間違いを犯した」と決めつけるのは傲慢というものです。
天才少年を生んだ母親はもっと天才だったとしてもおかしくありません。
何か別の考えがあって、正しくと答えた可能性は否定できないのです。そもそも少年の言葉には「たす」という言葉が入っていません。ツイートには「電車で数遊びをしている」とあります。
この母親が何故と答えたのかについて、実は親子は次の節で述べるような数遊びを行っていたのではないか?と妄想してみましょう。
とある数遊び
下の図のような状況からスタートする遊びを考えます。
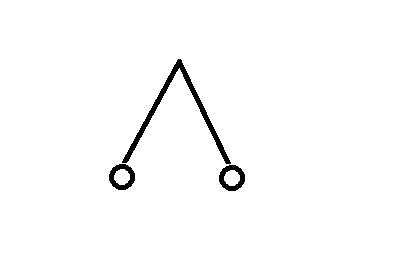
図に出てくる白丸の個数をカウントしていきます。すなわち、スタートの図からと定めます。
次のようなルールによって次のステップに進みます:
- 残っている白丸に ①上にあるもの, ②左にあるもの, の順に優先順位を付ける。
- 優先順位の高いものから順に、残っている白丸の個数(
個)だけ新しい白丸をくっつけていく。
- 一つの白丸に対して最大2つの新しい白丸を下の段にくっつけることができる。
- 2つの白丸が下にくっついた白丸は黒く塗りつぶす。
- 残っている白丸の個数を
とする。
言葉で説明すると難しいので実際に図で確認してみましょう:
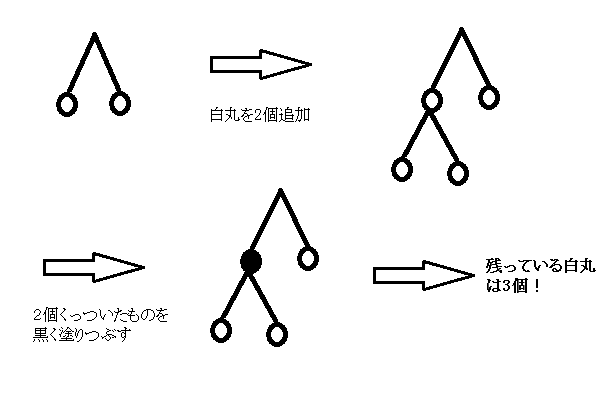
図から分かるようにです。とりあえず、
まで遊んでみましょう:
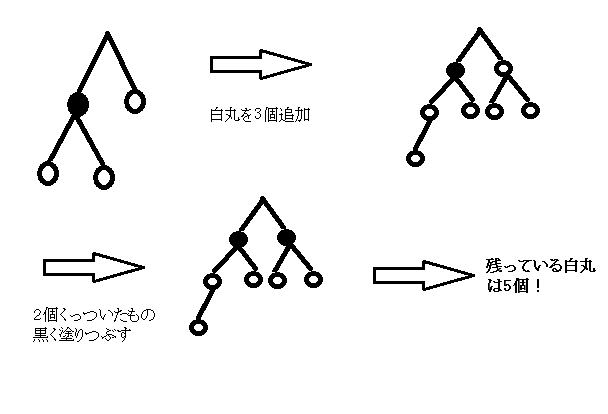
より。
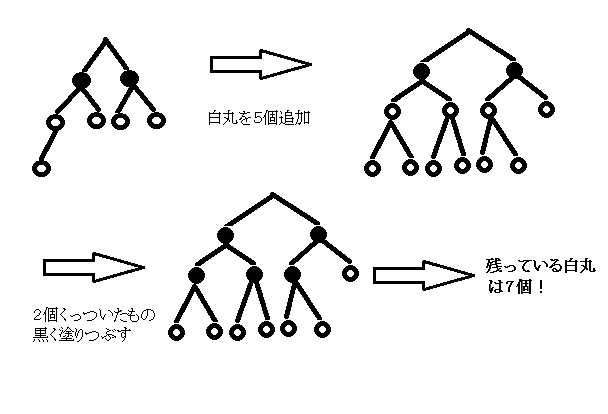
より。
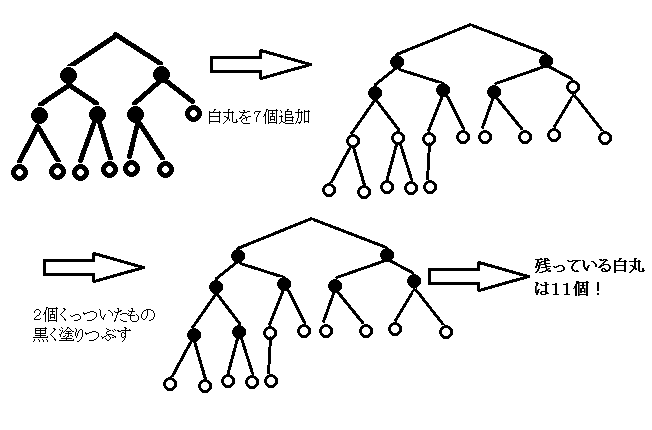
より。
何だって!?素数が現れているではないか!!
次はもしかして?
と思ったそこの奥さん!それは早とちりです。
実は、天才少年の母親が言ったようになのです!!
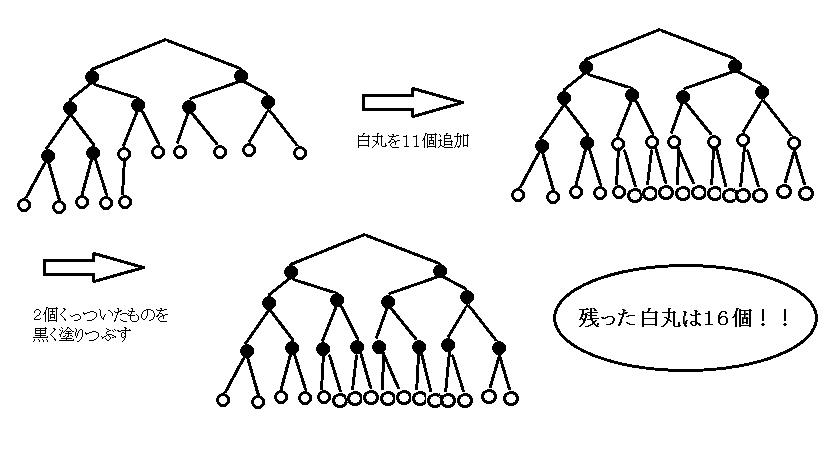
さて、親子はこのような数列遊びをしていた可能性があるのではないでしょうか?
母親「そうね、
たす
は
だね。」
というのは図を子どもと見ながら、あるいは思い浮かべながら単にをカウントしていたのでしょう(最初の2つの白丸から延びるのがそれぞれ3個と2個である。強引な推論ですが(汗))。
そして、となるにも関わらず、「この数列は素数になるに違いない!」と早とちりして
「じゅーさん!」
と言ってしまった子どもに対し、
「違うでしょ、()
でしょ。」
と母親は修正を促したのです。
しかしながら、一度素数だと勘違いしてしまった少年は
「じゅーなな、じゅーきゅ、にじゅーさん、にじゅーきゅ、さんじゅいち!」
と止まることが出来なくなってしまって、母親は
「この子の数学力はまだまだね。」
と呆れてしまったのであった。。。
冒頭のツイートはもしかしたらこのようなエピソードだったんじゃないか?と妄想してしまったせきゅーん(当ブログ管理人)なのでした。
数列の満たす漸化式
実はこの数列は次のような単純な漸化式を満たします:
によって定まる。ここで、はGauss記号。
この定理を証明しましょう。
各


はType Aであり、
はType Bです。
Typeについては数遊びの定義から次が分かります:
次に、数列を「
をカウントする図において新しく増えた黒丸の個数」と定義します。
すると、数遊びのルールから
であることが分かります。
また、次の補題が成り立つことも数遊びのルールから分かります:
最後に次の補題が必要になります:
証明. に関する数学的帰納法で証明する。
のときは正しい。
で正しいと仮定して
のときに証明する。
が偶数のとき
が偶数ならば
も偶数なので、帰納法の仮定によって
は偶数でType Aである。よって、補題1より
はType Aである。また、
が奇数ならば
は奇数で、帰納法の仮定により
は奇数でType Bとなる。よって、補題1より
はやはりType Aである。
が奇数の場合も同様に示す。 Q.E.D.
定理の証明. に関する数学的帰納法で証明する。
のときは正しいので、
で正しいと仮定して
のときに証明する。
が偶数のとき
は整数なので、
が成り立つ。帰納法の仮定により、これはに等しい。一方、補題2より
なので、
。よって、
のときも主張は正しい。
が奇数かつType Aのとき 補題3より
は偶数でなければならない。従って、
および
が成り立つ。よって、帰納法の仮定により
となるが、補題2および①よりこれはに等しい。
が奇数かつType Bのとき 補題3より
は奇数でなければならない。従って、
および
が成り立つ。よって、帰納法の仮定により
となるが、補題2および①よりこれはに等しい。 Q.E.D.
 のデータ
のデータ
←素数!
←素数!
←素数!
←素数!
←素数!
←素数!
←素数!
←素数!
←素数!
←素数!
奇数になるようなが無数に存在することは容易に分かりますが、素数になるような
が無数に存在するかは非常に難しい問題だと思われます。
参考にしたウェブサイト
Integer Sequence A112088 by Simon Strandgaard.
この数列は私が考案したものではありません。