は合成数であるような最小のヘックス数です。
ヘックス数
一辺が個の点からなるような正六角形状に点を配置したときの個数を第
ヘックス数と言い、
で表します(中心付き六角数とも言います)。
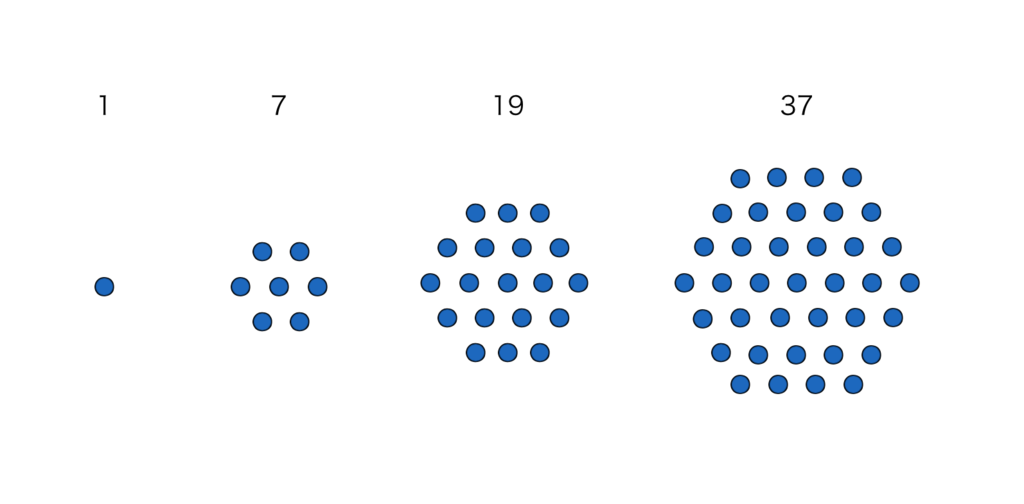
これを六角数と呼びたくなりますが、六角数という名称を持つ数はヘックス数よりも小さい数として昔から別の定義があるため使うことが出来ません。ヘックス(hex)は六角形の英語hexagonの省略形ですが、六角形の升目のことをヘックスと呼びます。また、ヘックスという名のボードゲームがあって例えば次のサイトで遊ぶことが出来ます*1: http://www.afsgames.com/hex.htm
ヘックスについては:
HEXの定理(1) - フィボナッチ・フリーク
HEXの定理(2) - フィボナッチ・フリーク
実はこのヘックスというゲームを用いたJordanの曲線定理の証明があって面白いのですが、それはまた別の機会に紹介したいと思います。
一万以下のヘックス数は次のようになっています:
ちなみに赤色の数は素数です。千以下だと約61.1%、一万以下でも約48.3%が素数で結構多いですね。
ヘックス数の一般項と天才的求め方
ヘックス数の一般項はで与えられます。これを求める方法は色々あると思いますが、例えば最初の図を見れば
と漸化式が求まります。しかしながら、次のようなある意味で天才的な
の求め方があります:
を正六角形状に配置した図は一辺が
個の点からなる立方体に見える。
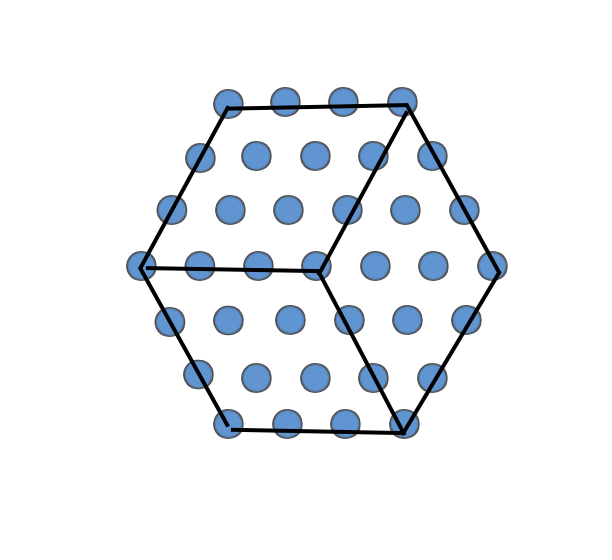
そして、「三次元空間に一辺が個の点からなる立方体状に点を配置したものから一辺が
個の点からなる立方体状に点を配置したものを取り除いた部分」をある角度から平面に投影したものが
と思えるため、
である。
は階差の形になっているため、望遠鏡和によって
が成り立つことが分かります。
*1:2019年中に削除されるようです。