次の有名定理の証明を解説します:
証明はたくさんありますし、短いものも知られていますが、今回は個人的に面白かった証明を採用します*1。
用語等
- 等差数列の初項・公差・長さ … 長さのみ馴染みがないかもしれませんが、しばしば項数と呼ばれるものです。等差数列(arithmetic progression)をAPと略記します。初項・公差・長さがそれぞれ
のAPを
と表示します。長さが
のAPを
-APと呼びます。
- 正の整数
に対し、集合
を
と略記します。
- 正の整数
に対して、
の
-シフト
を
で定義します。これを区間と表現することがあります。
- 正の整数
に対し、
の
色塗り分けとは写像
のことを言います*2。要は
の元が色で、
に対する
が
の色です。同様に、正整数
に対して、写像
のことを
の
-シフトの
色塗り分けとよびます。
- 同色
-AP … 考察中の塗り分けに対し構成する数の色が全て同じであるような長さ
のAPのこと。
- 車輪 …
を正の整数とします。このとき、半径
、スポーク数
、ハブ
の車輪とは、
個の
-APの組
のことを言います。各
に対して、(
)-AP
のことをスポークと言います(
のときはスポークなし)。

- カラフルな車輪 … スポークがそれぞれ同色(
)-APで、ハブと各スポークが全て相異なる色になっているような車輪のこと。すなわち、
色塗り分け
に対して(
)、或る相異なる色
が存在し、
,
が任意の
および
に対して成り立つ(車輪の設定は直前のものを用いた)。

戦略・証明の流れ
で言えれば、任意の
で言えるのは主張の性質上明らかです。次の主張も自明ですが、認識しておくことは非常に重要です:
定理の証明は長さに関する数学的帰納法で行います。つまり、同色(
)-APの存在は仮定されているので、それを上手く用いて同色
-APを作ることができれば勝ちです。
しかし、それは簡単には実行できそうにはありません。同じ色で個連続で数が等間隔に並んでくれていたとしても、そう都合よくもう一つ隣の数が同じ色をしてくれているとは限らないからです。
ただ、少し嬉しいこととして、材料になる同色()-APはいくらでも用意できます。というのも、任意の正整数
を取って
を考えれば、これを
等分した各集合は平行移動の原理によって同色(
)-APを含む*3ので、
個の同色(
)-APを得ることができます。とは言っても、いくら同色(
)-APがあってもどいつもこいつも同色
-APに延長できない可能性は否定できません。
そこで一旦同色-APを作ることは諦めて、半径
のカラフルな車輪をスポーク数について帰納的に製造していきます(つまり証明の全体的な構造は二重帰納的!)。実はこのカラフルな車輪製造についても平行移動の原理が成り立つので、一度製造方法を習得できれば同スポーク数のカラフルな車輪はいくらでも大量に生産することが可能になります。大量のカラフルな車輪を用いてスポーク数がもう一つ多いカラフルな車輪を製造します。
その製造過程で重要になるのが「に関する帰納法なので、
の場合は塗り分けの数が何であっても成立すると仮定されている」点です。
同スポーク数(本とします)の大量生産されたカラフルな車輪はそれぞれ配色はバラバラなものになっているでしょう。
それら選ばれし個のカラフルな車輪を材料にすれば上手くスポーク数
のカラフルな車輪を作ることが出来るのです(新しいスポークは
個の車輪のハブ達をつなぎ合わせて作る!)。
もう少し正確に言うと、製造過程で運良く同色-APを見つけることが出来たならばその時点で勝利なので、運悪く同色
-APを見つけることが出来なかった場合にはカラフルな車輪のスポーク数を増やすことが出来るという仕組みです。
ところが!色には限りがありますので、どれだけ数達が同色-APを発見されるのを拒もうとも、スポーク数が
に到達した時点で或るスポークはハブと同色にならざるを得ません(鳩ノ巣原理!)。つまり、そのスポークとハブからなるAPこそ同色
-APなのです!
証明
に関する数学的帰納法で証明する。
のときは自明である(任意の正整数は任意の塗り分けに対して同色
-AP)。そこで、
とし、
のときに定理の主張が成り立つと仮定する。すなわち、任意の正整数
に対して或る正整数
が存在して、任意の
の
色塗り分けに対して、
は同色(
)-APを含むと仮定する。
任意の正整数を取って、以下これを固定する。或る正整数
が存在して
が必ず同色
-APを含むことを示せばよい。そのために、次の主張を示す:
- 同色
-AP または
- 半径
、スポーク数
のカラフルな車輪
の少なくとも一つを含む。
これはに関する帰納法で証明する。
の場合:
と取れる。実際、帰納法の仮定により
は同色(
)-APを含むので、それをスポークとしてハブとなる数を一つ付け加えれば半径
、スポーク数
の車輪となる。スポークの色とハブの色が等しければ同色
-APであり、異なればカラフルな車輪である。
で主張が成立すると仮定する。
とし、
で
に対する主張が成立することを示す。
の
色塗り分け
を固定する。
の中の
個の区間
を考えよう*4。いずれかの区間が同色-APを含んでいれば証明は完了するため、いずれの区間も同色
-APを含んでいない場合を考える。このとき、主張は平行移動の原理が成り立つものなので、各区間は半径
、スポーク数
のカラフルな車輪を含む(これらの車輪は
の元によって管理されていることに注意)。すなわち、任意の
に対して或る
及び相異なる
色
が存在して、
が成り立つ(が車輪のハブで、
がスポーク。ハブの色が
でスポークの色が
)。
ここで、別の塗り分け
を考える。全単射があるので、これは
色塗り分けである。
の定義により、
は
についての同色(
)-APを持つ。

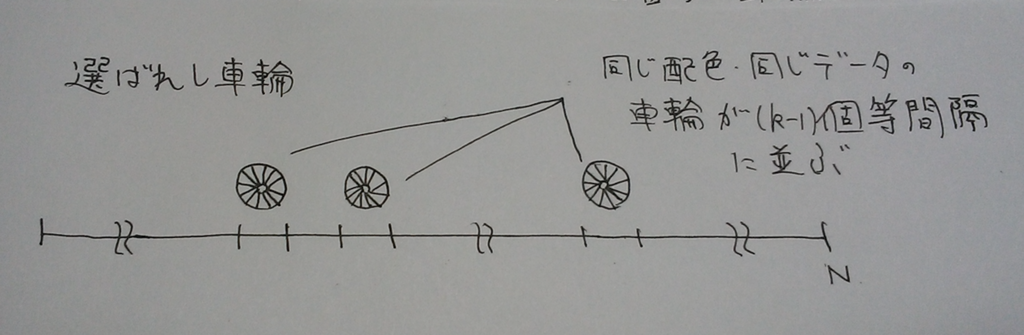
それをとし、色が
であったとする。このとき、
なる同じデータを持つようなカラフルな車輪が
個存在することになる。それらを用いて半径
、スポーク数
の車輪を次のように構成する:
- ハブ:
- 新しいスポーク:
- 旧スポークから作られる
本のスポーク(対角的に数を結ぶ):
- 車輪:


であり、
なので
。また、
である。スポークを構成する数についても
なので(は
を構成する数なので
の元であることに注意)、この車輪はちゃんと
内に存在する。各スポークの色を確認しよう。
新しいスポークの色: 各に対して
旧スポークから作られるスポークの色:各に対して
よって、各スポーク一つずつは同色で塗られており、は相異なる色であったので、作った車輪のスポーク同士の色は相異なることがわかった。
ハブの色は何かは分からない。もし、あるスポークの色と同じであるならば、すなわち、
なる
が存在すれば、
は同色
-APである。また、もし
がどの
とも相異なるのであれば、作った車輪はカラフルな車輪になっている。以上で主張が証明された。
主張よりと取れることがわかる。実際、
は任意の
色塗り分けに対して同色
-APまたは半径
、スポーク数
のカラフルな車輪を含むが、もし後者が成立しているならば色が
色存在する必要があり矛盾する。よって、
は必ず同色
-APを含む。 Q.E.D.
歴史
どうやらBaudet*5の予想として知られていた問題を、ArtinとSchreierとの(少なくない)コミュニケーションの後、若き数学者van der Waerdenが解決したようです*6。元々のBaudet予想は次のような形をしていると思われます*7。
この予想はBaudetの死の直前、1921年に定式化されたとする文献がありました。van der Waerdenの定理からBaudet予想が従うことはすぐ分かります。
vdWの定理  Baudet予想の証明
Baudet予想の証明
vdWの定理を仮定して背理法によって証明する。自然数全体の個のクラス分けであって(
)、どのクラスも「任意の長さの等差数列を含む」という性質を満たさないものがあったと仮定する。すると、どのクラスについても、そのクラスに所属する等差数列の長さは有界である*9。従って或る
が存在して、どのクラスも
-APを含まない。このとき、
をクラス分けによって塗り分ければ、vdWの定理によって同じクラスに所属する
-APが存在する。これは矛盾。 Q.E.D.
van der Waerdenは素朴な主張(=Baudet予想)を強める(=vdWの定理)ことによって帰納法による証明を可能にしたのですが、実はBaudetの予想からvdWの定理を導出することができます!*10 記号を正整数全体集合とします。
Baudet予想  vdWの定理の証明
vdWの定理の証明
Baudet予想を仮定して背理法によって証明する。vdWの定理を否定して、或る正整数、狭義単調増大正整数列
、
の
色塗り分け
が存在して、
は
に対する同色
-APを含まないと仮定する。
鳩ノ巣原理によって、狭義単調増大正整数列が存在して
が成り立つことがわかる。
再び鳩ノ巣原理によって、の部分狭義単調増大正整数列
が存在して
が成り立つことがわかる。
これを繰り返して、狭義単調増大正整数列の列
であって、任意のに対して
が成り立つようなものを選択する。ここで、狭義単調増大数列を考えて、写像
を
で定義する。
このとき、は
によって
個のクラスに分けることができるので、Baudet予想によって任意の長さの等差数列を含むクラスが存在する。つまり、或る
-AP
が存在して
が成り立つ。任意のに対して
なので、
とすれば
となって、が同色
-APを含まないという仮定に矛盾する。 Q.E.D
*1:Taoの"A quantitative ergodic theory proof of Szemerédi's theorem"のarXiv版の付録。用語や一部の議論を変更しています。
*2:全射を仮定した方が色全部を使っていて言葉に合いますが、ここでは仮定しません。
*3:「含む」は「考えている集合の個の元であって同色(
)-APをなすものが存在する」の意味。他の場所で使用している「含む」も同様の用法。
*4:一番大きい数はでこれは
以下。
なので各区間に交わりはない。
*5:Pierre Joseph Henry Baudet (1891/1/22 - 1921/12/25)はオランダ人数学者。チェロ、ピアノ、チェスなどが好きで、幾つかの言語を喋ることができたようです。
*6:彼はこの成果で数学者としての名声を得、その数年後、27歳のときに(ArtinとNoetherの講義に基づいて)代数学の有名な教科書を出版しています。
*7:正確な歴史はかなり難しそうです。van der Waerdenは論文タイトルにBaudetの名前を入れていますが(従ってBaudetへのcreditを与えたのはvan der Waerden)、Baudetについては殆ど何も知らなかった?また、Soiferの本によれば(まだちゃんと読めていません)、Ramsey以前にRamsey理論的定理を得ていたIssai Schurもこの予想にたどり着いていたようです(二つへ分ける場合)。
*8:正の整数でなければならないわけではありません。「整数全体」としても同じことが言えます。
*9:-APを含めば、
なる任意の正整数
に対する
-APも含むことになるから。
*10:従って、Baudet予想とvan der Waerdenの定理は同値です。驚きました。