講演スライドを公開します。スライド番号や間違い等は再構成・修正してあります。
スライドはKeynoteで作成し、数式はLaTeXiTを利用して作成しました。
1枚目

2枚目

3枚目

4枚目

5枚目

6枚目*1

7枚目

8枚目*2

9枚目

10枚目

11枚目*3

12枚目*4

13枚目*5

14枚目*6

15枚目*7
16枚目*8

17枚目*9

18枚目*10

19枚目

20枚目

21枚目*11

22枚目

23枚目*12

24枚目
25枚目

26枚目

27枚目*13

28枚目
29枚目

30枚目

31枚目*14

32枚目

33枚目*15

34枚目*16
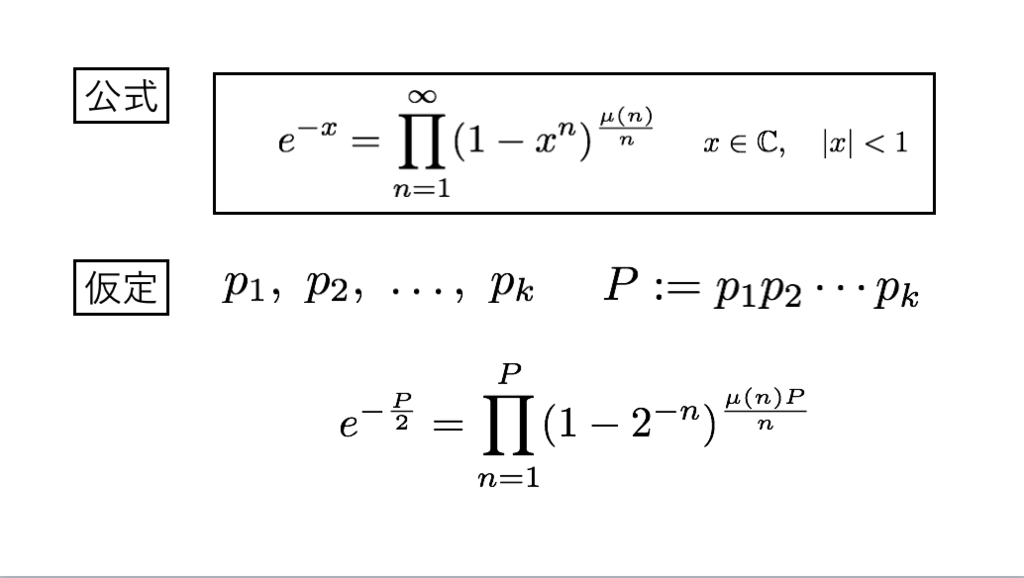
35枚目*17

36枚目
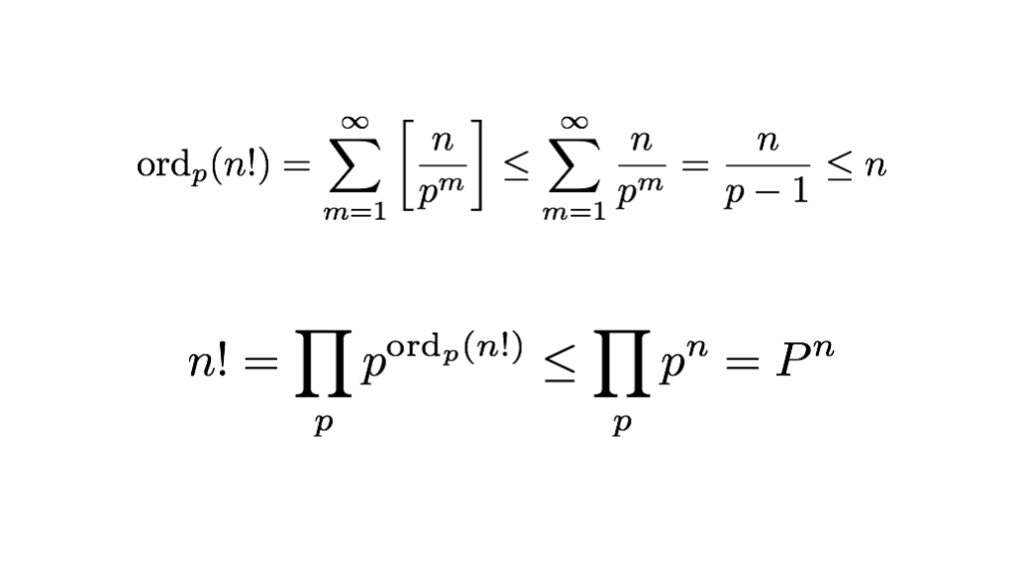
37枚目
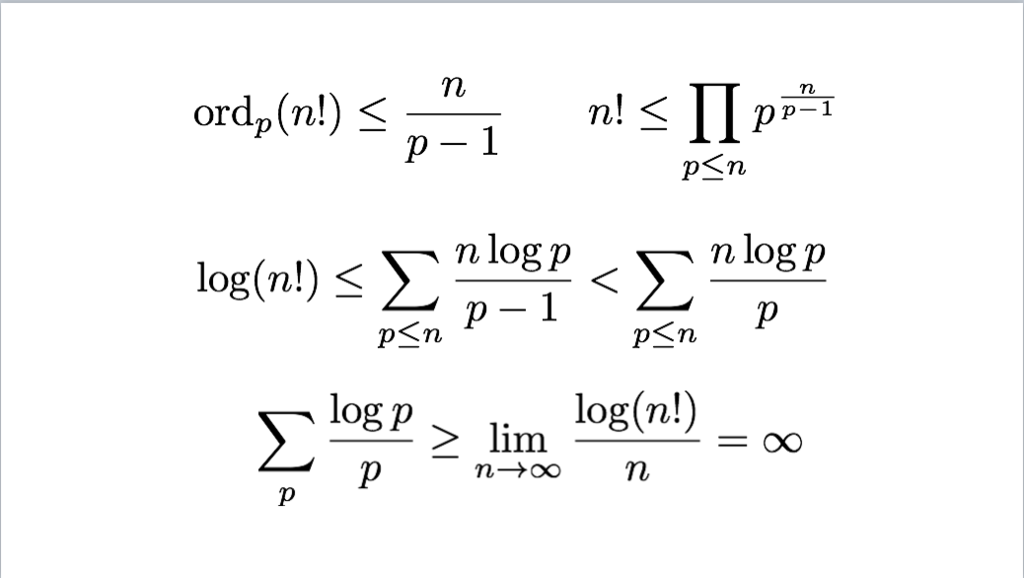
38枚目

39枚目*18

40枚目
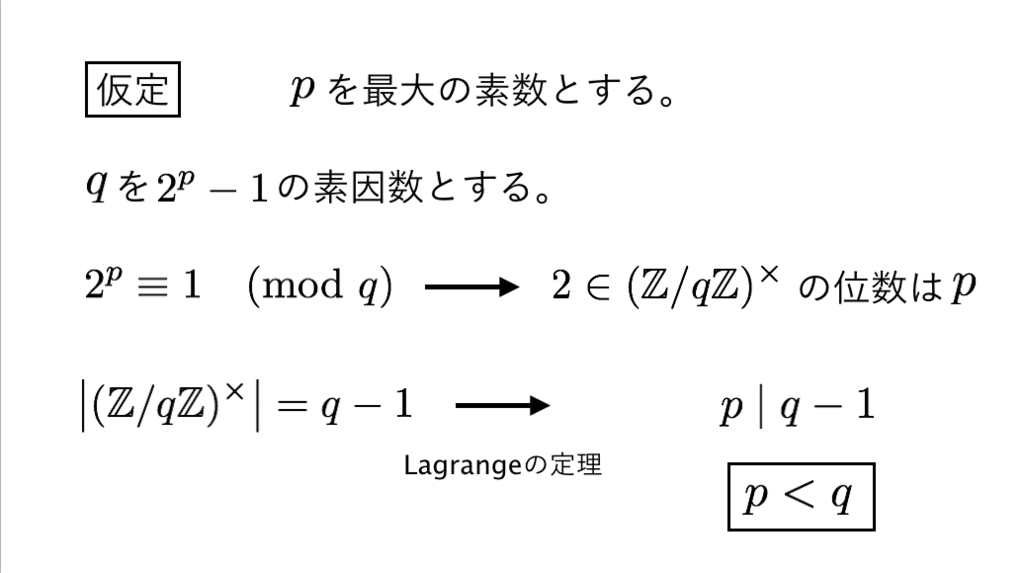
41枚目*19

42枚目*20

43枚目*21

44枚目*22

45枚目

46枚目*23
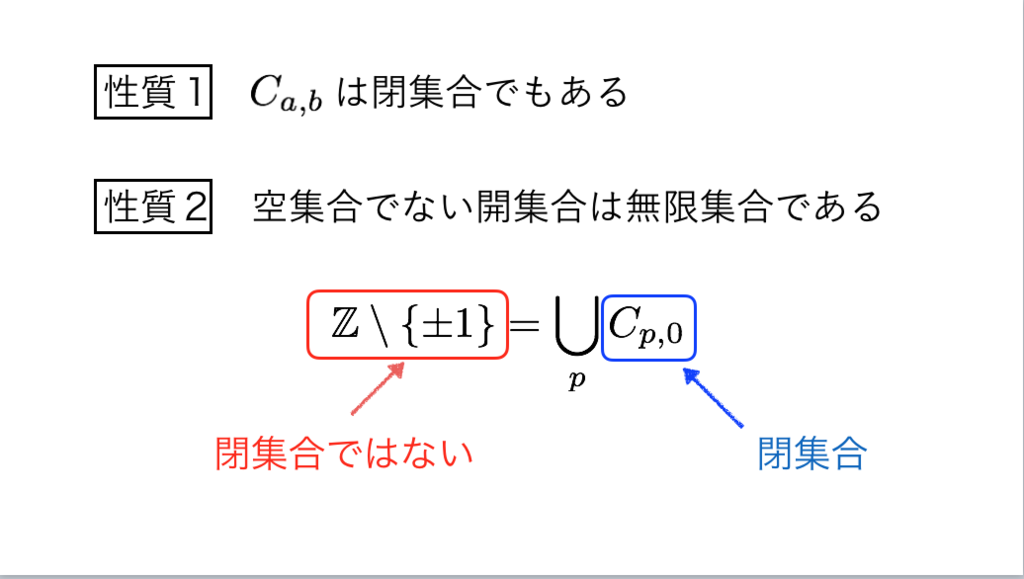
47枚目

48枚目*24

49枚目

50枚目
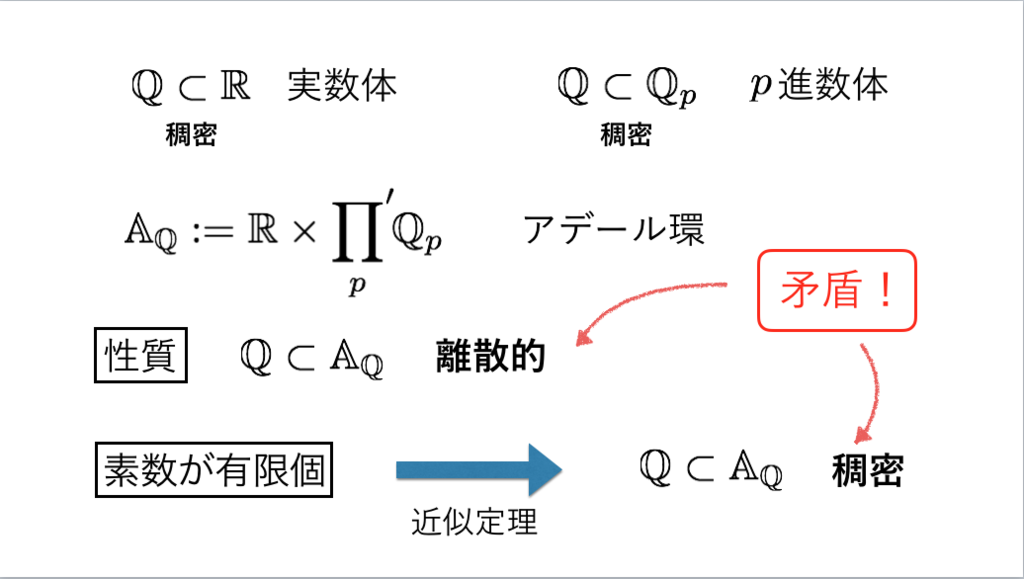
51枚目*25

52枚目*26

53枚目

54枚目*27

55枚目*28

56枚目
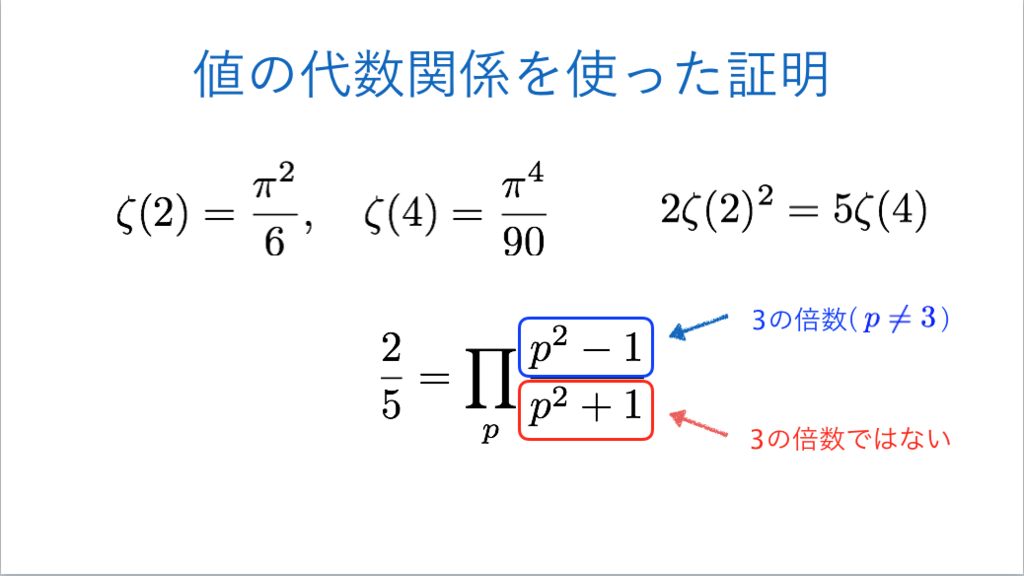
57枚目*29

58枚目

59枚目

60枚目*30

61枚目*31
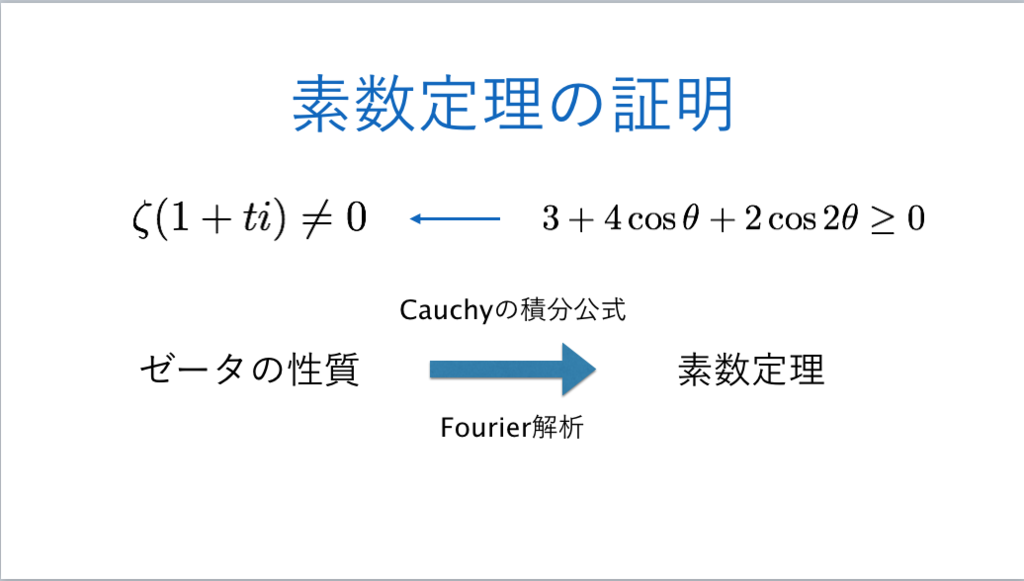
62枚目*32

63枚目

64枚目

65枚目

66枚目

67枚目*33

68枚目

69枚目

70枚目*34
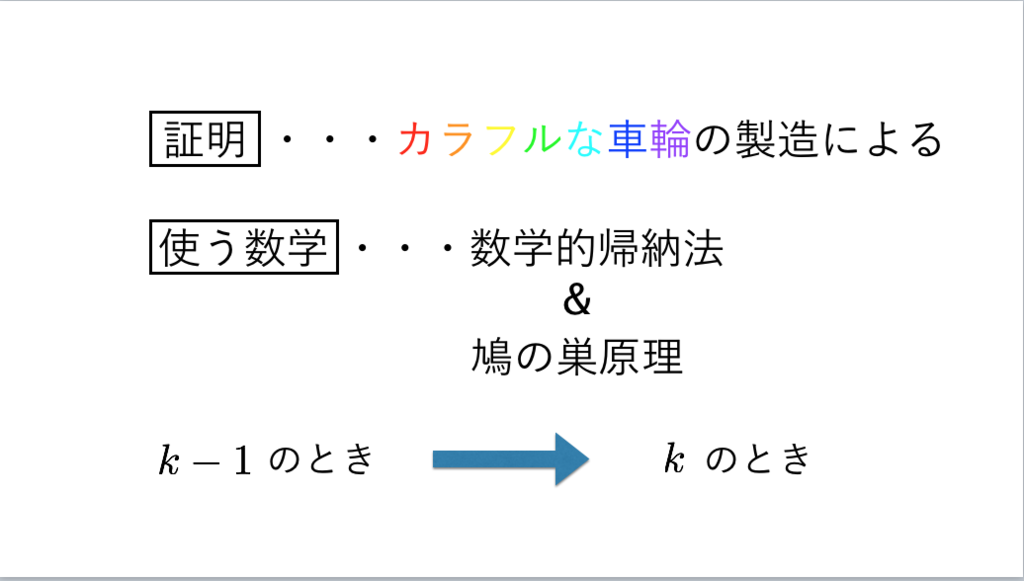
71枚目
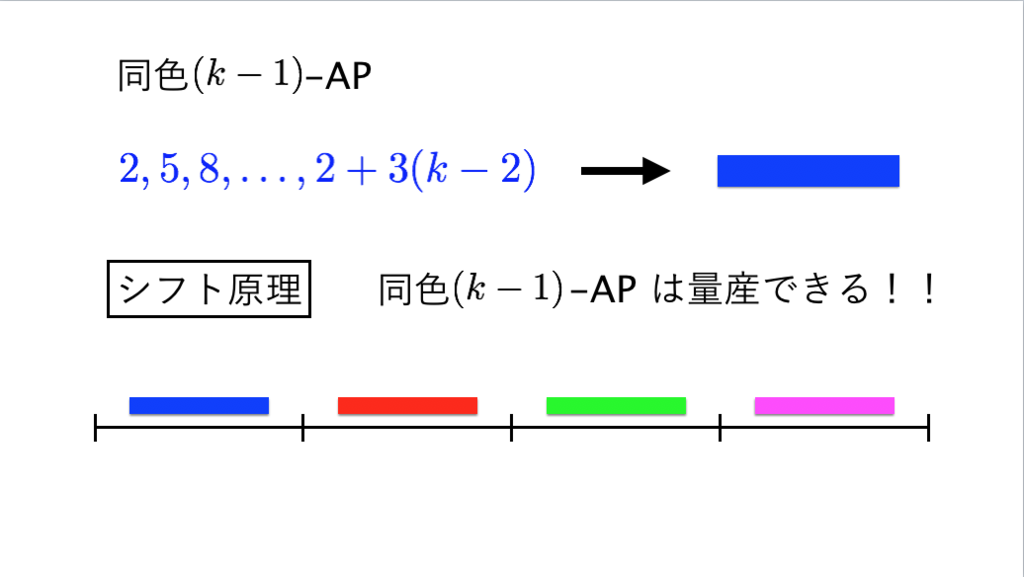
72枚目
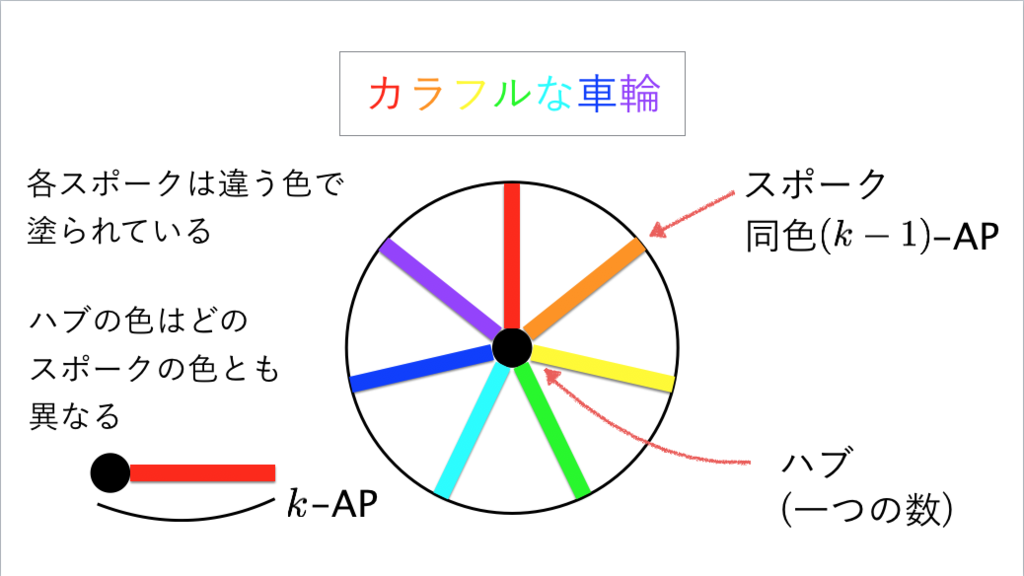
73枚目

74枚目
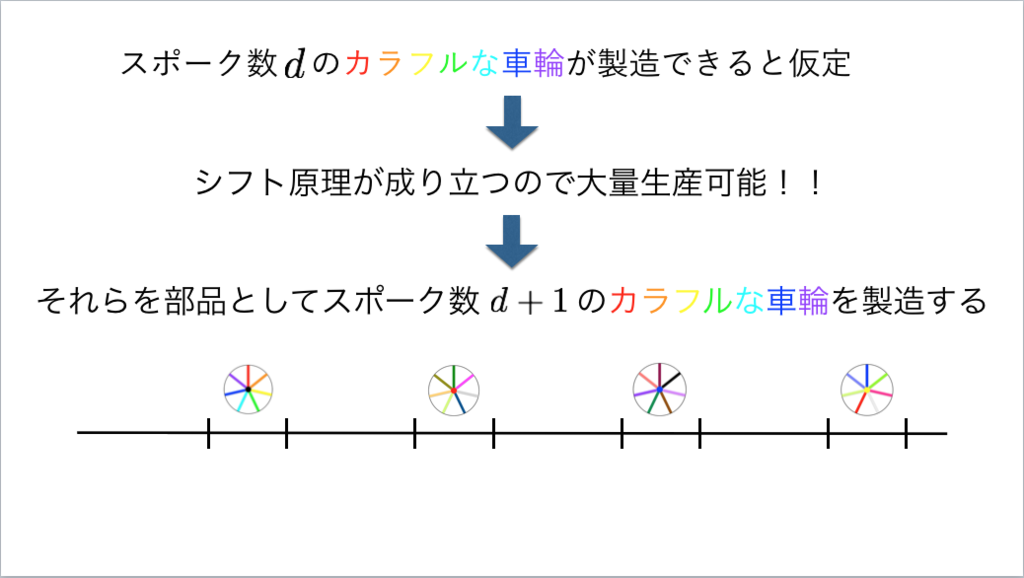
75枚目
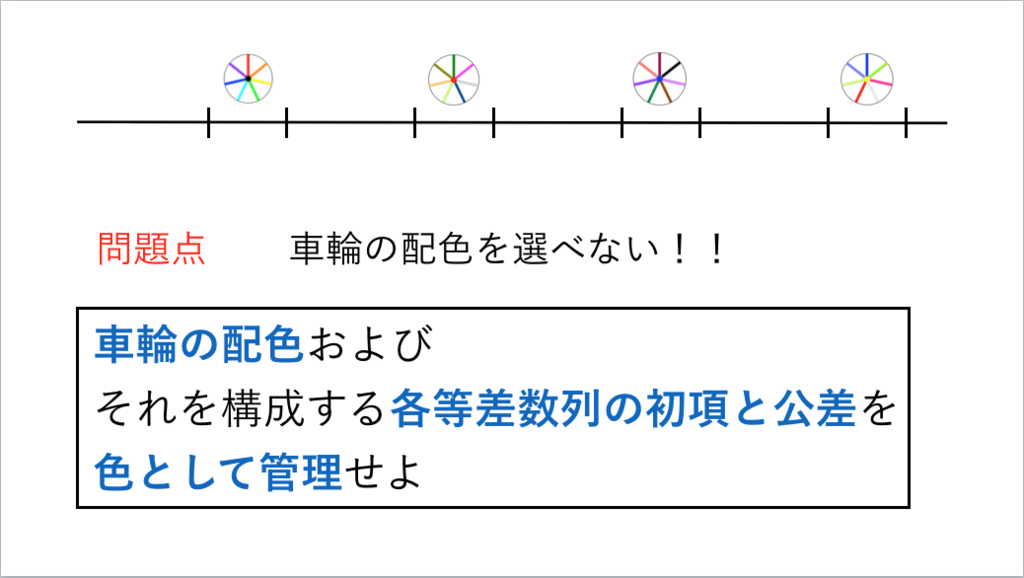
76枚目*35
77枚目*36
78枚目
79枚目
80枚目
81枚目*37

82枚目

83枚目

84枚目*38

85枚目*39

86枚目

87枚目*40

88枚目*41

89枚目*42

90枚目*43

91枚目*44

92枚目*45

93枚目

94枚目

95枚目*46

96枚目

97枚目*47
98枚目*48

99枚目

100枚目*49

101枚目*50

102枚目*51

103枚目*52

104枚目*53
105枚目
106枚目*54

107枚目*55

108枚目*56

109枚目*57

110枚目*58
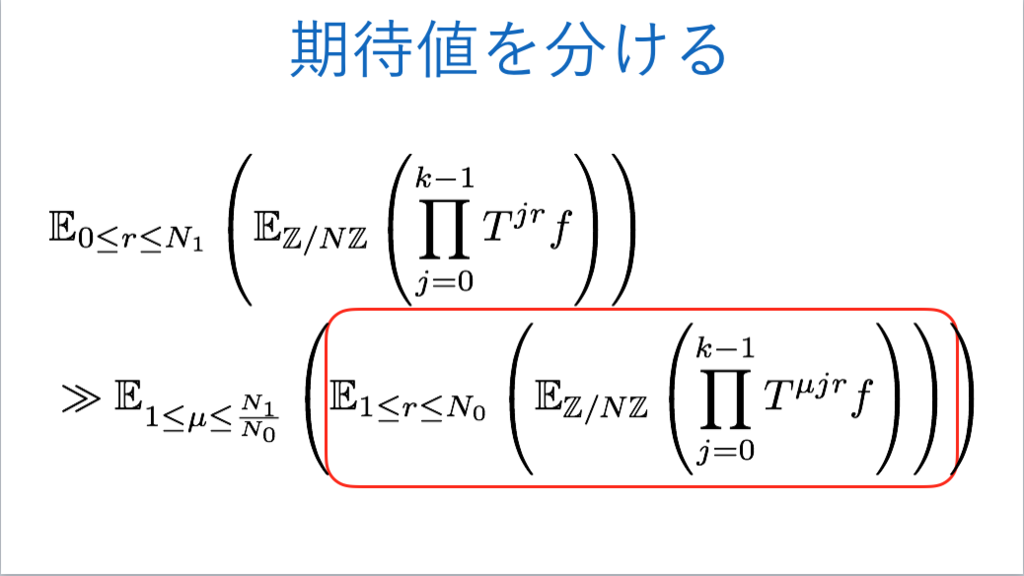
111枚目*59

112枚目*60

113枚目*61
114枚目
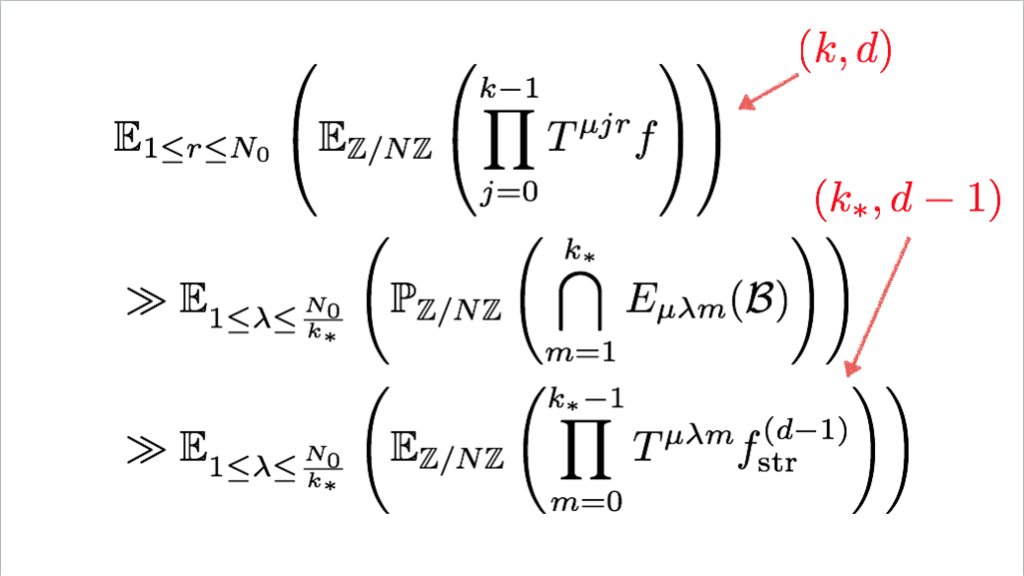
115枚目

116枚目*62
117枚目
118枚目*63

119枚目*64

120枚目

121枚目
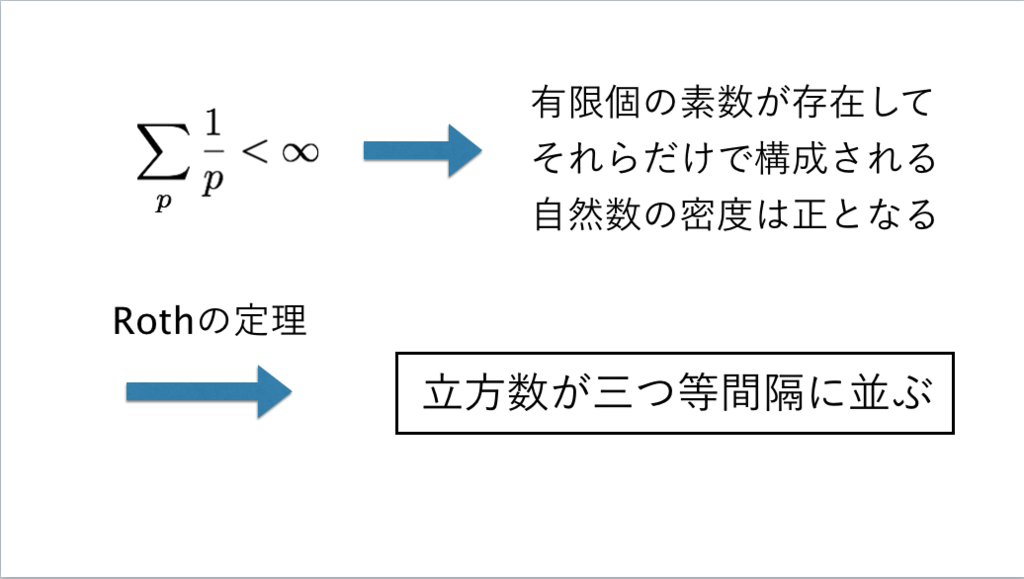
122枚目

123枚目*65
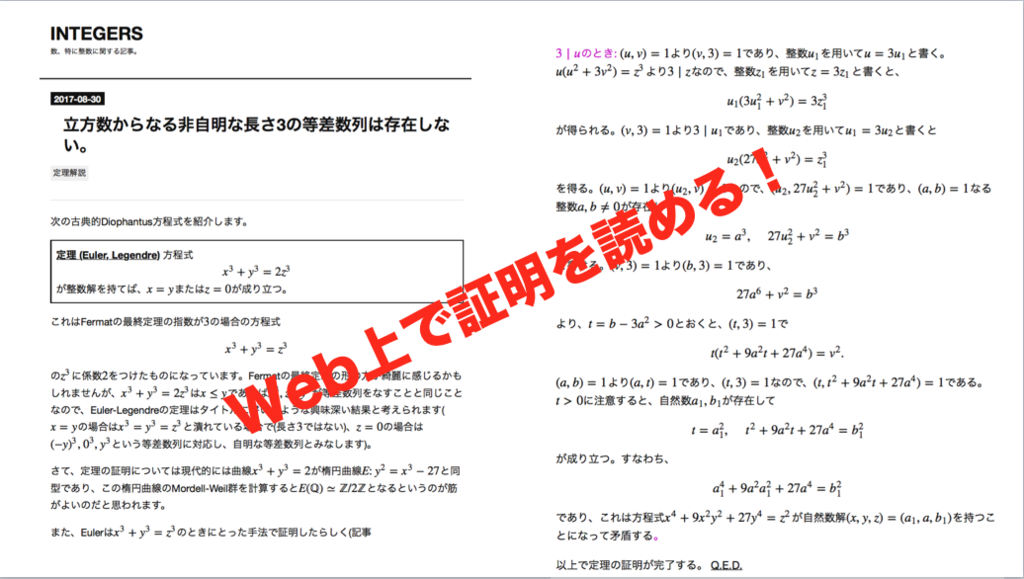
124枚目*66

125枚目

126枚目

127枚目

128枚目

129枚目*67

130枚目

131枚目*68

132枚目

133枚目

134枚目

135枚目

136枚目*69

137枚目*70

138枚目*71

139枚目

140枚目

141枚目*72

142枚目*73
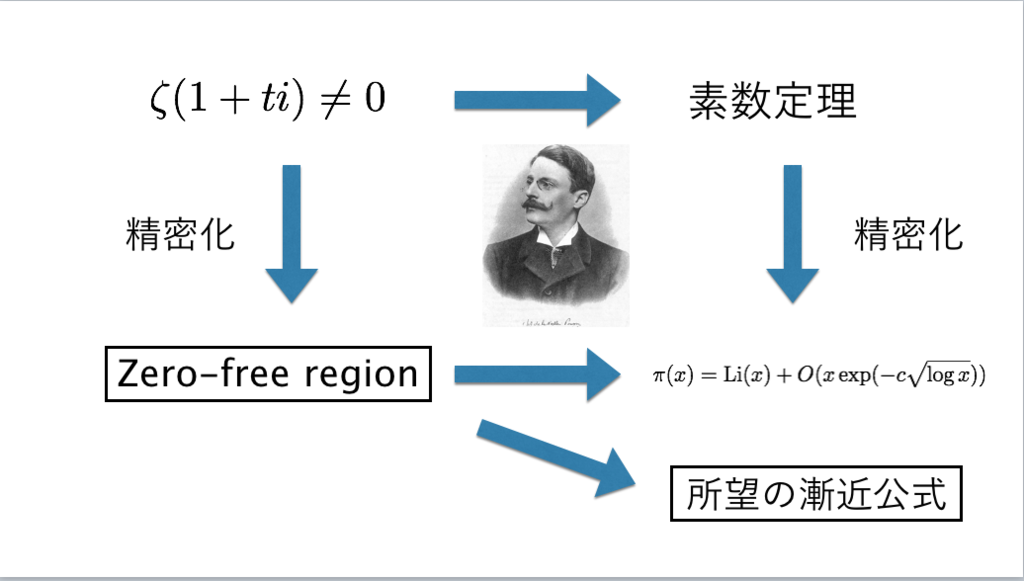
143枚目*74

144枚目

145枚目

146枚目
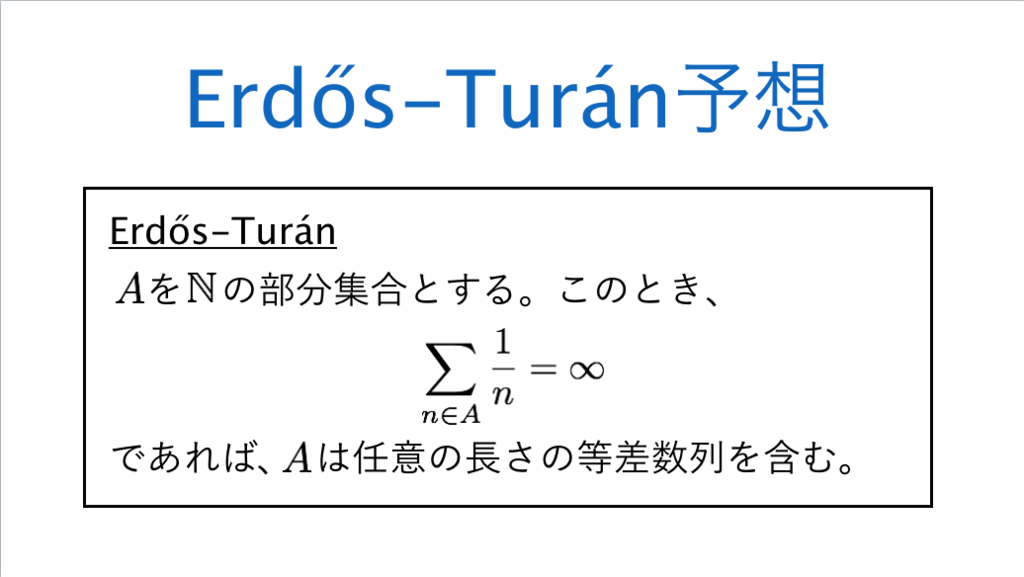
147枚目*75

148枚目*76
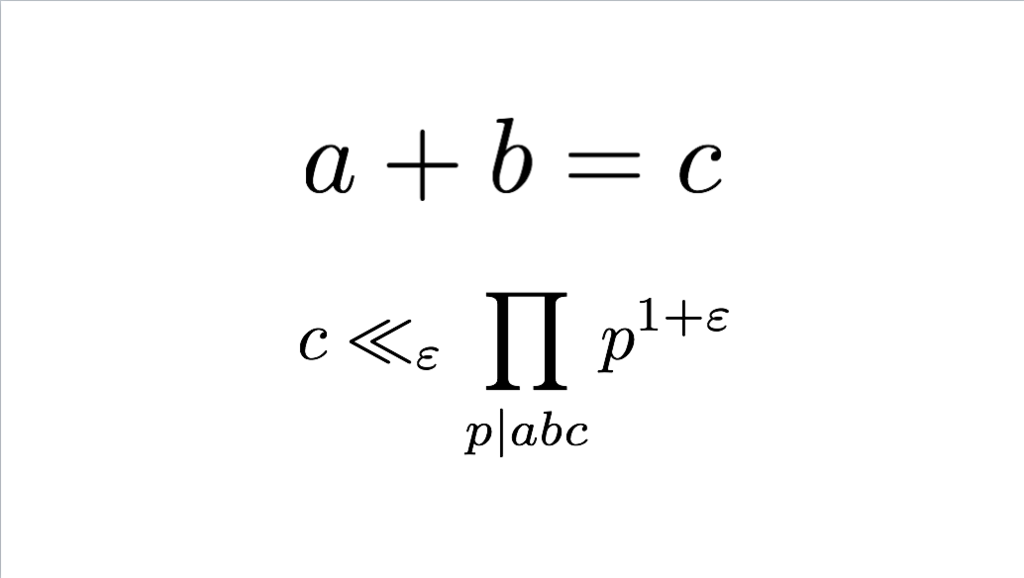
149枚目
*1:このスライドは本番では飛ばしてしまいました。「最高の講演にしたい!」という意気込みでしたが、発表練習は結局一度も出来なかったのでミスが出てしまいました。好きな素数を選んでいたのですが。cf. ジェノッキ素数が17しか存在しないことの証明 - INTEGERS
*2:素因数分解の一例ですが、好きな素数を使っています。指数があった方がいいかなと思って
に二乗もつけてみました。cf. 関-ベルヌーイ数 - INTEGERS, 1213:素数大富豪における二枚出し最強素数 - INTEGERS
*3:いくらでも大きい素数が存在するということで、大きい素数を一つ紹介してみましたが。
*4:実は、当ブログでバズった特別な素数です:やたらすごい素数 - INTEGERS
*5:肖像画が特徴的で、初めて見た時に笑いのツボに入ってしまいました。
*6:素数は無数にあるけれど、実は全然ない。素数密度零補題 - INTEGERS
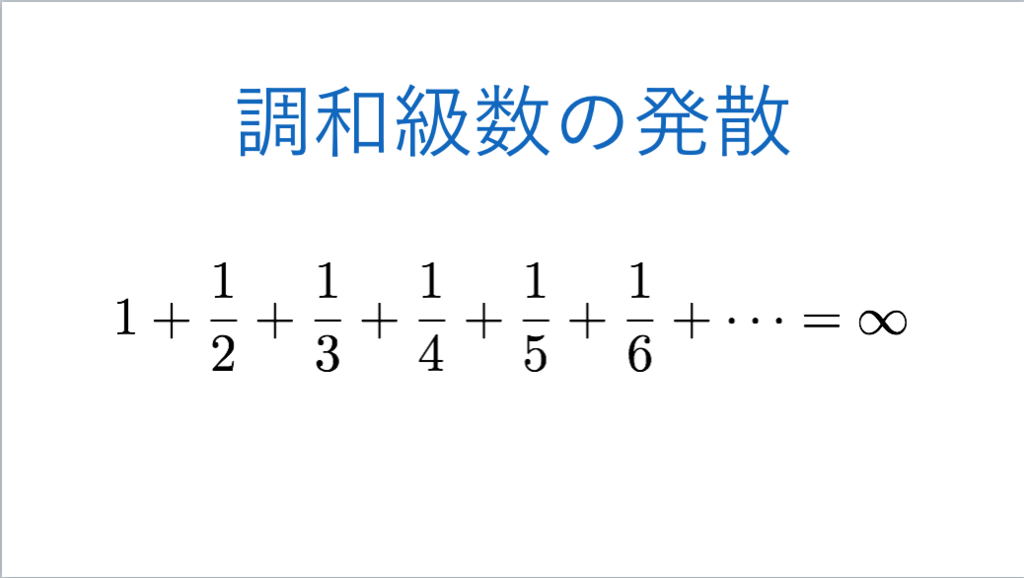
*7:16843:ウォルステンホルム素数、調和数、調和級数、オイラーの定数 - INTEGERS, 調和級数の発散証明 - INTEGERS
*8:Eulerの命日9/18はLegendreの誕生日と一致しています。この次のスライドは掲載を省略しますが、素数の逆数和の発散の原論文を紹介しました(Theorema 19)。原論文のPDFはこちら→E72 -- Variae observationes circa series infinitas
*9:素数は意外にある。
*10:ここでもスライドを飛ばすミスをしてしまいましたが、これは喋った方がいいだろうと思い、戻って解説しました。1801241230056600523以下の素数の逆数和は4を超える - INTEGERS
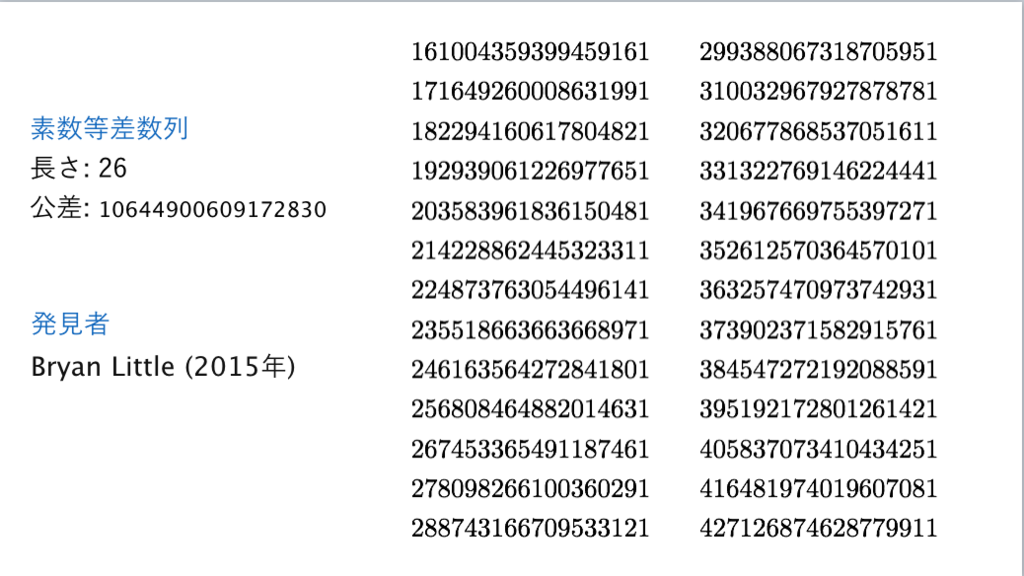
*11:私の講演のキャッチフレーズが「ガウス素数定理予想から周年」でした。素数定理 - INTEGERS
*12:長さから長さ
にとんでるのはこれらが各長さの素数等差数列の最大項が最小である例だからで、長さ
の最小例も
から始まるもので長さ
の例に含まれています。
*13:Taoが生まれた1975年に色を付けているのは、Szemerédiの定理の論文の出版年という記念すべき年に生まれたからですが、講演では言及し忘れました。テレンス・タオ - Wikipedia, ベン・グリーン - Wikipedia
*14:掲載は省略しますが、Euclidの原論の該当ページの写真のスライドがこの一つ前にありました。
*15:eが無理数であることの5通りの証明 - INTEGERS
*16:解説記事:eの無限積表示と素数の無限性 - INTEGERS
*17:ここから37枚目までの解説記事:2015の階乗を10の502乗で割った数の一の位は? - INTEGERS
*18:tsujimotterさんによる解説記事:群論におけるフェルマーの小定理 - tsujimotterのノートブック
*19:Lawrence C. Washington - Wikipedia
*20:当ブログではまだ書いてないですが、とりあえず代数的整数論の演習問題レベルです。
*21:PIDでない数体の整数環については42枚目の演習問題を根拠に素イデアルの無限性が従い、そこから有理素数の無限性も導出できるという視点です。つまり、素数が無数に存在しないと類数が以上の数体は存在し得なかったという解釈ができます。
*23:解説記事:有限位相空間の個数 - INTEGERS
*24:「付値」は自明でない付値の同値類
*25:この次のスライドは掲載を省略しますが、原論文を紹介しました(Theorema 8)。原論文のPDFはこちら→E72 -- Variae observationes circa series infinitas
*26:ここから紹介する三つの証明の解説記事:リーマンゼータ関数 - INTEGERS 質問を受けましたが、別証明として紹介しているものは全て循環論法ではありません。循環論法になるケースについてはeが超越数であることの証明 - INTEGERS
*27:バーゼル問題の高校数学範囲内で分かる証明 - INTEGERS
*28:左側については先ほどのリーマンゼータ関数の記事。右側はπ:Never Ending Number~ラマヌジャンのMysteriousな公式~ - INTEGERS
*29:先ほどのリーマンゼータ関数の記事
*30:証明の解説記事:メビウス関数 - INTEGERS
*31:ゼータ関数の零点とリーマン予想 - INTEGERS
*33:ラムゼーの定理と6人の問題 | 高校数学の美しい物語
*34:このスライドから始まる証明の解説記事:ファン・デル・ヴェルデンの定理 - INTEGERS
*35:積分記号を使っていることに気づいた人はいるかな??
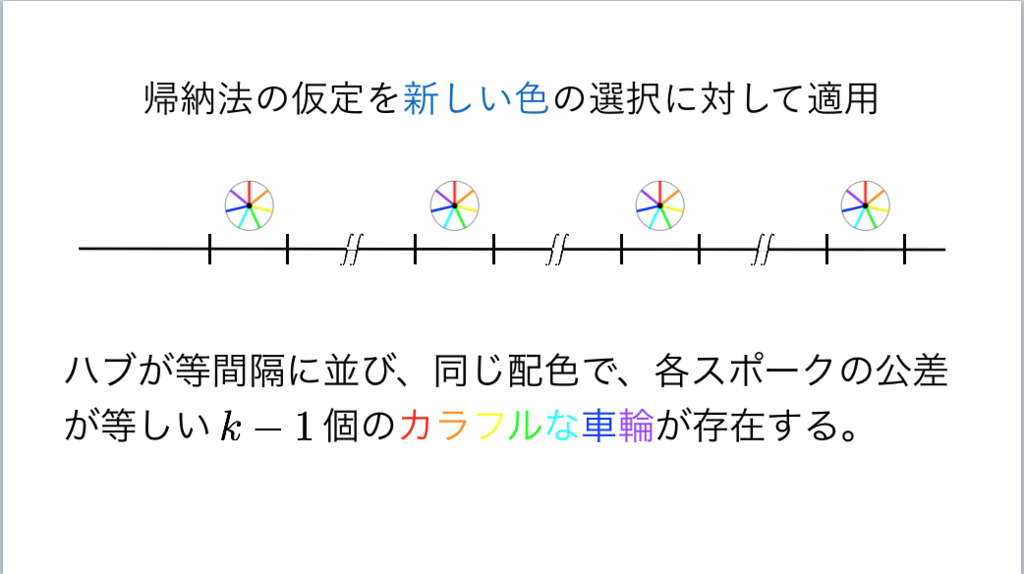
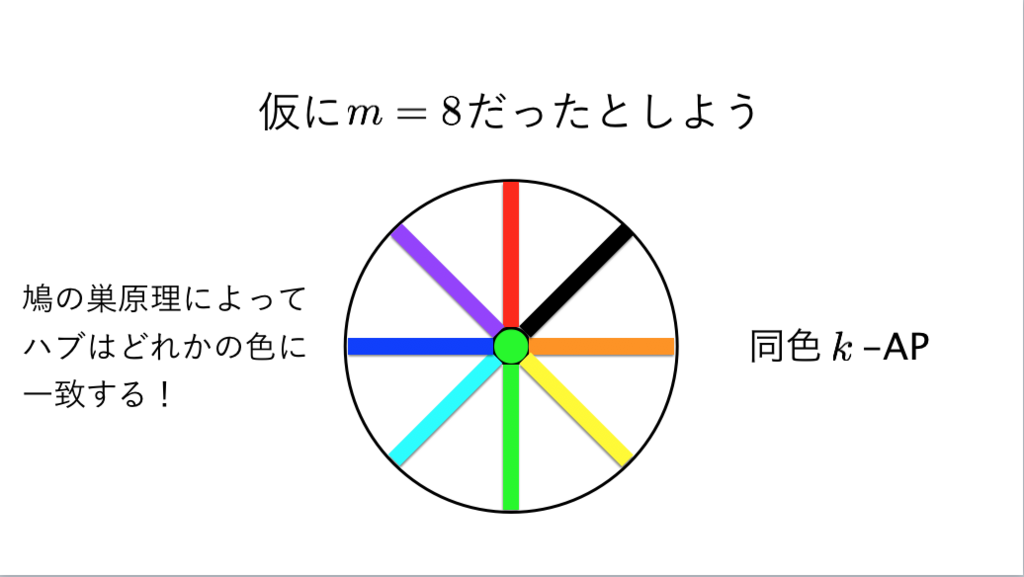
*36:ハブを貫いて新しいスポークを作る!
*37:ポール・エルデシュ - Wikipedia, Pál Turán - Wikipedia
*40:ロスによるエルデシュ・トゥーラン予想の解決 - INTEGERS
*41:Endre Szemerédi - Wikipedia
*42:掲載は省略しますが、この次のスライドで原論文に描かれている論理図を紹介しました。原論文:http://matwbn.icm.edu.pl/ksiazki/aa/aa27/aa27132.pdf
*43:ウィリアム・ティモシー・ガワーズ - Wikipedia
*44:Gowersの証明が2010年になっていました。申し訳ございません。
*45:このスライドから始まる証明はタオのセメレディ論文の§1, 2を読む - INTEGERSから解説が始まります。
*46:実際の証明では技術的理由によりは素数としています。
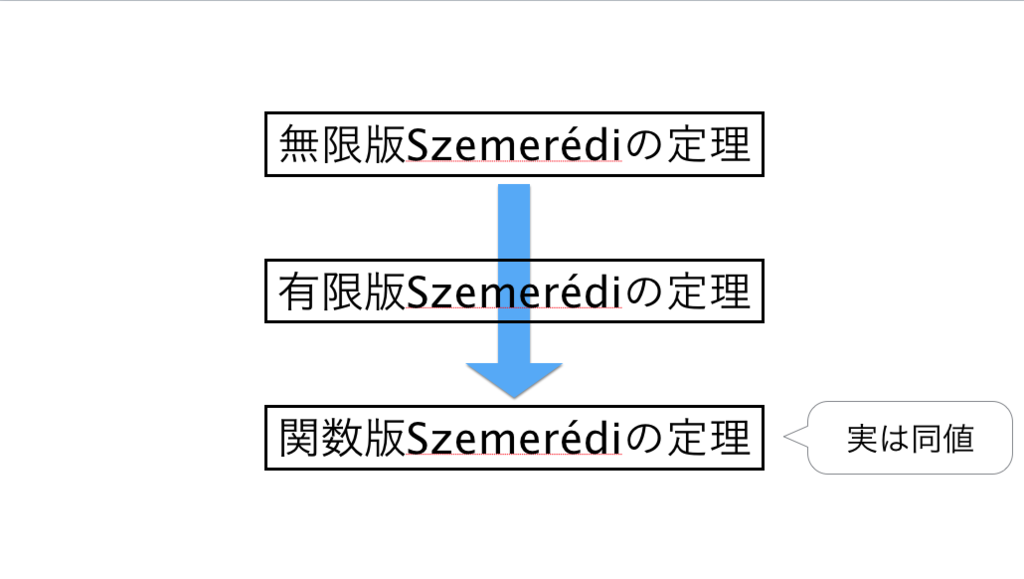
*47:矢印は言い換えの順番を表していて、証明が簡単な論理の方向は逆矢印となります。
*48:ランダム部分排除定理、構造化部分に対するSzemerédiの定理はTaoはそれぞれ一般化von Neumannの定理、構造化回帰定理と呼んでいます。タオのセメレディ論文の§3を読む - INTEGERS
*49:定義はタオのセメレディ論文の§4を読む - INTEGERS
*50:定義はタオのセメレディ論文の§5を読む (その一) - INTEGERS
*51:正確にはタオのセメレディ論文の§5を読む (その二) - INTEGERSの命題2。「生み出される」は気取りすぎでした。
*52:正確な主張は§3の記事に書いてあります。実際には 一つでは上手くいかず、
と
が必要。
*53:このスライドの正確な内容はタオのセメレディ論文の§6を読む (その二) - INTEGERS, タオのセメレディ論文の§6を読む (その三) - INTEGERS
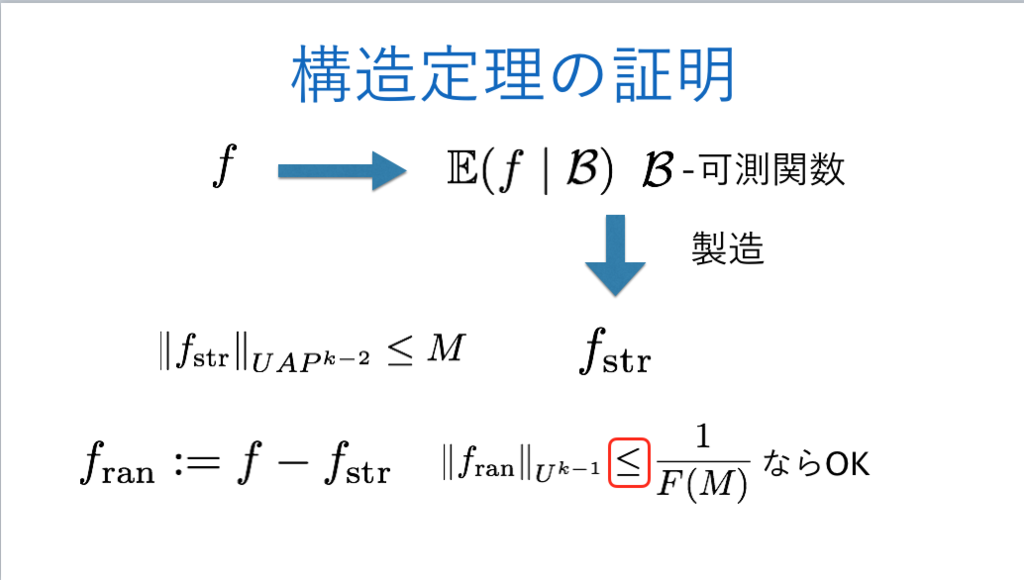
*54:実際には-加法族そのものに定義される量は複雑度。エネルギーの定義とエネルギー増加法についてはタオのセメレディ論文の§7を読む - INTEGERS。実際のエネルギー増加法は
-加法族のペアに関する複雑な形で定式化する必要があります。
*55:正確な証明はタオのセメレディ論文の§8を読む - INTEGERS
*56:正確な定義は§5(その一)の記事。
*57:正確な主張は§3の記事の「一様概周期関数の回帰性」
*58:ここでの分割は次の記事の⭐︎式:タオのセメレディ論文の§10を読む(その一) - INTEGERS
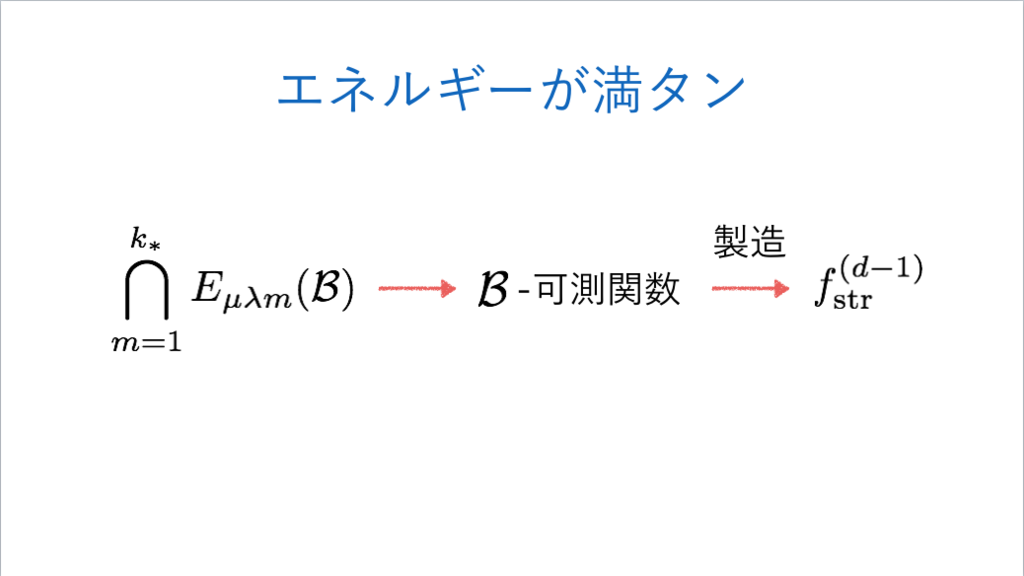
*59:-加法族は実際にはペアで考えることに注意して、その構成は§10(その一)の最後の方で行われています。エネルギーが満タンであるということはタオのセメレディ論文の§10を読む(その二) - INTEGERSで場合分けの形で記述されています。
*60:§9の内容をこのスライド一枚に閉じ込めて細かい点の解説はしませんでした。タオのセメレディ論文の§9を読む(その一) - INTEGERS, タオのセメレディ論文の§9を読む(その二) - INTEGERS
*61:これと次のスライドは§10(その二)の最後の方の計算。
*62:重たいSzemerédiの定理の証明の解説が終わり、Green-Taoの高みに入る前に休憩の話を挿入しました。
*63:素数の無限性の一風変わった証明 - フィボナッチ・フリーク
*64:Andrew Granville - Wikipedia
*65:立方数からなる非自明な長さ3の等差数列は存在しない。 - INTEGERS
*66:このスライドから始まる証明の概略はグリーン・タオ論文の§1, 4を読む - INTEGERSから解説が始まります。
*67:擬ランダム測度の定義と次のスライドの定理についてはグリーン・タオ論文の§3を読む - INTEGERS
*68:証明の詳細はSzemerédiの定理と同様として省略しました。このスライドについてはグリーン・タオ論文の§8を読む(その一) - INTEGERSに詳しく、§8(その二)までに擬ランダム測度に対するSzemerédiの定理が証明されます。
*69:-トリックに関する解説はグリーン・タオ論文の§2を読む - INTEGERS
*70:Green-Tao測度の構成についてはグリーン・タオ論文の§9を読む(その一) - INTEGERS
*71:擬ランダム測度であることを示すには線形形式条件に対応する式(Goldston-Yıldırım型定理A)と相関条件に対応する式(Goldston-Yıldırım型定理B)を証明する必要がありますが、ここでは前者のみ記述しています。
*72:積分表示を得る計算はグリーン・タオ論文の§10を読む(その一) - INTEGERSで実行されます。補題3やその後の無限積の分割が-トリックが効いてくる箇所です。
*73:ゼータ関数に関する解析は最後の記事で実行されます:グリーン・タオ論文を読み終える - INTEGERS
*74:謎の数学者バウデットが死の直前に遺した真珠 - INTEGERS
*75:素数の織り成す構造に関する第三の勝利にたどり着いたのかもしれない。
*76:に依存する正の数
が存在して
が成り立つことを
で表している。ABC予想についてはABC予想 - INTEGERS